σ-代数
设

为
非空集合
,

中的元素是

的子集合,满足以下条件的
集合系

称为

上的一个
σ代数
:
-

在

中;
-
如果一个集合

在

中,那么它的
差集
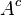
也在

中;
-
如果有可数个集合

都在

中,那么它们的
联集
也在

中。
用数学语言来表示,就是
不借助逻辑符号的话,也可以使用如下更简洁的定义:设

为
非空集合
。则

上的一个
σ代数
是指其
幂集
的子集合

对有限个
差集
、
交集
跟可数个并集这三种运算都依然属于

,也就是说

对这三运算是封闭(closed)的 。
在测度论里

称为一个可测空间。 集合族

中的元素,也就是

的某子集,称为可测集合。而在概率论中,这些集合被称为
随机事件
。
例子
-
有两个σ-代数的简单例子,它们分别是:
-

上含集合最少的σ代数

;和 -

上含集合最多的σ代数是

的
幂集

。
-
-
假设集合

,那么

是集合

上的一个σ代数。这也是所有包含
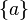
的σ代数中最“小”的一个。
概率空间
概率空间
(
Ω
,
F
,
P
)是一个总测度为1的
测度空间
(即
P
(
Ω
)=1).
第一项
Ω
是一个非空
集合
,有时称作“样本空间”。Ω 的集合元素称作“样本输出”,可写作ω。
第二项
F
是样本空间
Ω
的
幂集
的一个非空子集。
F
的集合元素称为
事件
Σ。事件Σ是样本空间
Ω
的子集。集合
F
必须是一个
σ-代数
:
-

; -
若

,则

; -
若

,
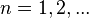
,则

(
Ω
,
F
)合起来称为
可测空间
。事件就是样本输出的集合,在此集合上可定义其概率。
第三项
P
称为
概率
,或者
概率测度
。这是一个从集合
F
到实数域
R
的函数,

。每个事件都被此函数赋予一个0和1之间的
概率值
。
概率测度经常以
黑体
表示,例如

或

,也可用符号”Pr”来表示。
分布函数的性质
对于特定的随机变量

,其分布函数

是单调不减及右连续,而且

,

。这些性质反过来也描述了所有可能成为分布函数的函数:
设
![F:[-\infty,\infty] \to [0,1], F(-\infty)=0, F(\infty)=1](https://upload.wikimedia.org/math/1/2/8/1283a9612a1acc8eac7e2bfb982414ab.png)
且单调不减、右连续,则存在概率空间
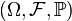
及其上的随机变量
X
,使得
F
是
X
的分布函数,即

设

为
概率测度
,

为
随机变量
则函数
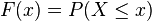
(
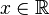
) 称为

的概率分布函数.如果将

看成是数轴上的随机点的坐标,那么,分布函数

在

处的函数值就表示

落在区间
![(-\infty,x]](https://upload.wikimedia.org/math/b/2/7/b27ac59ac8e050f8343b712b19ae8f71.png)
上的概率。
二项分布
在
概率论
和
统计学
中,
二项分布
是
n
个
独立
的是/非试验中成功的次数的
离散概率分布
,其中每次试验的成功
概率
为
p
。这样的单次成功/失败试验又称为
伯努利试验
。实际上,当
n
= 1时,二项分布就是
伯努利分布
。二项分布是
显著性差异
的
二项试验
的基础。
概率质量函数
一般地,如果随机变量
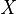
服从参数为
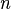
和

的二项分布,我们记

或

.n次试验中正好得到
k
次成功的概率由
概率质量函数
给出:
对于
k
= 0, 1, 2, …,
n
,其中
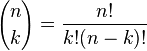
是
二项式系数
(这就是二项分布的名称的由来),又记为
C
(
n
,
k
),
n
C
k
,或
n
C
k
。该公式可以用以下方法理解:我们希望有
k
次成功(
p
k
)和
n
−
k
次失败(1 −
p
)
n
−
k
。然而,
k
次成功可以在
n
次试验的任何地方出现,而把
k
次成功分布在
n
次试验中共有C(
n
,
k
)个不同的方法。
在制造二项分布概率的参考表格时,通常表格中只填上
n
/2个值。这是因为
k
>
n
/2时的概率可以从它的补集计算出:
因此,我们要看另外一个
k
和另外一个
p
(二项分布一般不是对称的)。然而,它的表现不是任意的。总存在一个整数
M
,满足
作为
k
的函数,表达式
ƒ
(
k
;
n
,
p
)当
k
<
M
时单调递增,
k
>
M
时单调递减,只有当(
n
+ 1)
p
是整数时例外。在这时,有两个值使
ƒ
达到最大:(
n
+ 1)
p
和(
n
+ 1)
p
− 1。
M
是伯努利试验的最可能的结果,称为
众数
。注意它发生的概率可以很小。
累积分布函数
累积分布函数
可以表示为:
其中

是小于或等于
x
的
最大整数
。
它也可以用
正则化不完全贝塔函数
来表示:
期望和方差
如果
X
~
B
(
n
,
p
)(也就是说,
X
是服从二项分布的随机变量),那么
X
的
期望值
为
方差
为
这个事实很容易证明。首先假设有一个伯努利试验。试验有两个可能的结果:1和0,前者发生的概率为
p
,后者的概率为1 −
p
。该试验的期望值等于
μ
= 1 ·
p
+ 0 · (1−
p
) =
p
。该试验的方差也可以类似地计算:
σ
2
= (1−
p
)
2
·
p
+ (0−
p
)
2
·(1−
p
) =
p
(1 −
p
)
.
一般的二项分布是
n
次独立的伯努利试验的和。它的期望值和方差分别等于每次单独试验的期望值和方差的和:
正态分布又叫高斯分布
正态分布的定义
有几种不同的方法用来说明一个随机变量。最直观的方法是
概率密度函数
,这种方法能够表示随机变量每个取值有多大的可能性。
累积分布函数
是一种概率上更加清楚的方法,请看下边的例子。还有一些其他的等价方法,例如
cumulant
、
特征函数
、
动差生成函数
以及cumulant-
生成函数
。这些方法中有一些对于理论工作非常有用,但是不够直观。请参考关于
概率分布
的讨论。
概率密度函数

正态分布
的
概率密度函数
均值为

方差
为

(或
标准差

)是
高斯函数
的一个实例:
-
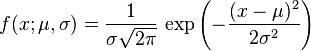
。
(
请看
指数函数
以及

.
)
如果一个
随机变量

服从这个分布,我们写作

~

. 如果
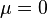
并且
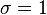
,这个分布被称为
标准正态分布
,这个分布能够简化为
-
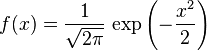
。
右边是给出了不同参数的正态分布的函数图。
正态分布中一些值得注意的量:
- 密度函数关于平均值对称
-
平均值与它的
众数
(statistical mode)以及
中位数
(median)同一数值。 -
函数曲线下68.268949%的面积在平均数左右的一个
标准差
范围内。 -
95.449974%的面积在平均数左右两个标准差

的范围内。 -
99.730020%的面积在平均数左右三个标准差

的范围内。 -
99.993666%的面积在平均数左右四个标准差
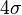
的范围内。 -
函数曲线的
反曲点
(inflection point)为离平均数一个标准差距离的位置。
累积分布函数

累积分布函数
是指随机变数

小于或等于

的概率,用概率密度函数表示为
正态分布的累积分布函数能够由一个叫做
误差函数
的
特殊函数
表示:
标准正态分布
的累积分布函数习惯上记为

,它仅仅
是指
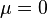
,
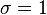
时
的值,
将一般正态分布用
误差函数
表示的公式简化,可得:
它的
反函数
被称为反误差函数,为:
该分位数函数有时也被称为
probit
函数。
probit
函数已被证明没有初等原函数。
正态分布的
分布函数

没有解析表达式
,它的值可以通过
数值积分
、
泰勒级数
或者
渐进序列
近似得到。
泊松分布
 横轴是索引 k ,发生次数。该函数只定义在 k 为整数的时候。连接线是只为了指导视觉。
概率质量函数
|
|
 横轴是索引 k ,发生次数。CDF在整数 k 处不连续,且在其他任何地方都是水平的,因为服从泊松分布的变量只针对整数值。
累积分布函数
|
|
| 参数 |
λ > 0( 实数 ) |
|---|---|
|
支撑集 |
k ∈ { 0, 1, 2, 3, … } |
|
概率质量函数 |

|
|
累积分布函数 |
(对于 |
|
期望值 |

|
|
中位数 |

|
|
众数 |

|
|
方差 |

|
|
偏度 |

|
|
峰度 |

|
|
信息熵 |
|
|
动差生成函数 |

|
|
特性函数 |

|
Poisson分布
,译名有
泊松分布
、
普阿松分布
、
卜瓦松分布
、
布瓦松分布
、
布阿松分布
、
波以松分布
、
卜氏分配
等,又称泊松小数法则(Poisson law of small numbers),是一种
统计
与
概率
学里常见到的
离散概率分布
,由
法国数学家西莫恩·德尼·泊松
(Siméon-Denis Poisson)在1838年时发表。
泊松分布适合于描述单位时间内随机事件发生的次数的概率分布。如某一服务设施在一定时间内受到的服务请求的次数,
电话交换机
接到呼叫的次数、汽车站台的候客人数、机器出现的故障数、
自然灾害
发生的次数、DNA序列的变异数、放射性原子核的衰变数等等。
泊松分布的
概率质量函数
为:
泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生率。
若
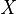
服从参数为

的泊松分布,记为

,或记为

.
性质
1、服从泊松分布的
随机变量
,其
数学期望
与
方差
相等,同为参数λ:E(X)=V(X)=λ
2、两个独立且服从泊松分布的
随机变量
,其和仍然服从泊松分布。更精确地说,若X ~ Poisson(λ1)且Y ~ Poisson(λ2),则X+Y ~Poisson(λ1+λ2)。
3、其
矩母函数
为:
泊松分布的来源(泊松小数定律)
在
二项分布
的
伯努利试验
中,如果试验次数n很大,二项分布的概率p很小,且乘积λ=
np
比较适中,则事件出现的次数的概率可以用泊松分布来逼近。事实上,二项分布可以看作泊松分布在离散时间上的对应物。
证明如下。首先,回顾
e
的定义:
二项分布的定义:
-

。
如果令
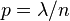
,

趋于无穷时

的极限:
最大似然估计
给定
n
个样本值
k
i
,希望得到从中推测出总体的泊松分布参数
λ
的估计。为计算
最大似然估计
值,列出对数似然函数:
对函数
L
取相对于
λ
的导数并令其等于零:
解得
λ
从而得到一个
驻点
(stationary point):
检查函数
L
的二阶导数,发现对所有的
λ
与k
i
大于零的情况二阶导数都为负。因此求得的驻点是对数似然函数
L
的极大值点:
例子
对某公共汽车站的客流做调查,统计了某天上午10:30到11:47来到候车的乘客情况。假定来到候车的乘客各批(每批可以是1人也可以是多人)是互相独立发生的。观察每20秒区间来到候车的乘客批次,共观察77分钟*3=231次,共得到230个观察记录。其中来到0批、1批、2批、3批、4批及4批以上的观察记录分别是100次、81次、34次、9次、6次。使用极大似真估计(MLE),得到

的估计为200/231=0.8658。
生成泊松分布的随机变量
一个用来生成随机泊松分布的数字(伪随机数抽样)的简单算法,已经由
高德纳
给出(见下文参考):
algorithm poisson random number (Knuth):
init:
Let L ← e−λ, k ← 0 and p ← 1.
do:
k ← k + 1.
Generate uniform random number u in [0,1] and let p ← p×u.
while p > L.
return k − 1.
尽管简单,但复杂度是线性的,在返回的值
k
,平均是λ。还有许多其他算法来克服这一点。有些人由Ahrens和Dieter给出,请参阅下面的参考资料。同样,对于较大的λ值,e
-λ
可能导致数值稳定性问题。对于较大λ值的一种解决方案是
拒绝采样
,另一种是采用泊松分布的高斯近似。
对于很小的λ值,逆变换取样简单而且高效,每个样本只需要一个均匀随机数u。直到有超过
u
的样本,才需要检查累积概率。
algorithm Poisson generator based upon the inversion by sequential search:[1]
init:
Let x ← 0, p ← e−λ, s ← p.
Generate uniform random number u in [0,1].
do:
x ← x + 1.
p ← p * λ / x.
s ← s + p.
while u > s.
return x.








![\operatorname{E}[X] = np](https://upload.wikimedia.org/math/9/e/d/9ed22d6f166c0c97bf4d3df33869a744.png)
![\operatorname{Var}[X] = np(1 - p).](https://upload.wikimedia.org/math/3/b/6/3b66ebdaf066b0f1478a5eddb0932d75.png)


![\Phi(z)=\frac12 \left[1 + \operatorname{erf}\left(\frac{z-\mu}{\sigma\sqrt2}\right)\right] .](https://upload.wikimedia.org/math/8/a/3/8a3995298cb2202cf5b57115a2b256cf.png)
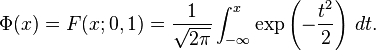
![\Phi(z)=\frac{1}{2} \left[ 1 + \operatorname{erf} \left( \frac{z}{\sqrt{2}} \right) \right].](https://upload.wikimedia.org/math/e/8/a/e8a87f901033e282bb77731fad761171.png)
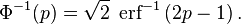



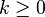


![\lambda[1 - \log(\lambda)] + e^{-\lambda}\sum_{k=0}^\infty \frac{\lambda^k\log(k!)}{k!}](https://upload.wikimedia.org/math/4/6/b/46bdca4f526c233b1dba425f44b0591b.png)


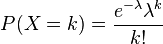
![M_X(t)=E[e^{tX}]=\sum_{x=0}^\infty e^{tX}\frac{e^{-\lambda}\lambda^x}{x!}=e^{-\lambda}\sum_{x=0}^\infty\frac{({e^t}\lambda)^x}{x!}=e^{{\lambda}(e^t-1)}](https://upload.wikimedia.org/math/a/4/0/a40546829ef4788b3ef7aa7e28cd1f13.png)

![\begin{align}\lim_{n\to\infty} P(X=k)&=\lim_{n\to\infty}{n \choose k} p^k (1-p)^{n-k} \\ &=\lim_{n\to\infty}{n! \over (n-k)!k!} \left({\lambda \over n}\right)^k \left(1-{\lambda\over n}\right)^{n-k}\\&=\lim_{n\to\infty}\underbrace{\left[\frac{n!}{n^k\left(n-k\right)!}\right]}_F\left(\frac{\lambda^k}{k!}\right)\underbrace{\left(1-\frac{\lambda}{n}\right)^n}_{\to\exp\left(-\lambda\right)}\underbrace{\left(1-\frac{\lambda}{n}\right)^{-k}}_{\to 1} \\&= \lim_{n\to\infty}\underbrace{\left[ \left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right) \ldots \left(1-\frac{k-1}{n}\right) \right]}_{\to 1}\left(\frac{\lambda^k}{k!}\right)\underbrace{\left(1-\frac{\lambda}{n}\right)^n}_{\to\exp\left(-\lambda\right)}\underbrace{\left(1-\frac{\lambda}{n}\right)^{-k}}_{\to 1} \\&= \left(\frac{\lambda^k}{k!}\right)\exp\left(-\lambda\right)\end{align}](https://upload.wikimedia.org/math/0/9/8/098dfaad42d2f1765750172fe9d0ad71.png)



