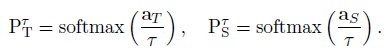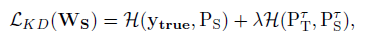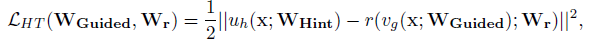最近读到一篇文章《
An On-device Deep Neural Network for Face Detection
》,讲的是苹果如何将基于深度学习的人脸识别方法应用到iPhone上,同时解决多任务并行及能耗的问题。文中提到了一个teacher-student network的概念。概括地讲,就是用一个更宽更复杂的,但是已经训练好的神经网络(教师网络),去训练另一个窄而深的网络(学生网络)。
在Adriana Romero等人2014年发表的paper《FitNets: Hints for Thin Deep Nets》中给出了一种参数较少的解决方案,以下内容主要翻译自这篇paper。
1、介绍
本文提出了利用深度的方法来解决网络压缩问题。我们提出了一种新的方法来训练窄而深的网络,叫做fitnet,来压缩较宽宽较浅(实际上仍然很深)的网络。这个方法根植于最近提出的KD算法(Knowledge Distillation)(Hinton和Dean,2014),并扩展了这个想法,使其适用于更窄、更深的学生网络模型。我们从老师网络的隐藏层中引入了intermediate-level hints来引导训练学生的过程,我们希望学生网络(FitNet)来学习中间表示(对教师网络的中间表示的预测)。Hints可以训练更薄、更深的网络。结果证实,拥有更深层的模型可以让我们获得更好的范性,同时这些模型很窄,有助于我们显著减轻计算负担。我们验证了我们的方法可以匹配或胜过老师网络的性能,同时需要更少的参数和运算。
2、KD算法(KNOWLEDGE DISTILLATION)
这个算法训练了一个学生网络,用一个来自更宽网络,教师网络的softened output。这样做的目的是让学生网络不仅能捕捉到由真实的标签提供的信息,但也包括由教师网络学习的更精细的结构。这个框架可以总结如下。
举个例子,让T成为一个教师网络,它的输出是softmax PT=softmax(aT),它是教师的前软最大激活的向量。在这种情况下,教师模型是一个单独的网络,代表了输出层的加权和,而如果教师模型是一个集合,PT或是aT结果是通过不同网络的平均输出得到的(分别用于算术或几何平均)。让S成为一个包含参数 WS 和输出概率 PS=softmax(aS) 的学生网络,as是学生网络的pre-softmax输出。学生网络将接受训练,使其输出PS与教师的输出PT类似,以及真正的标签ytrue。由于PT可能与样本真实标签的一个热代码表示非常接近,因此引入了一个放松τ > 1来减轻教师网络输出所产生的信号,从而在培训过程中提供更多的信息。当与教师的软输出(PT)相比较时,同样的放松也适用于学生网络(PS)的输出:
然后训练学生网络以优化下面的损失函数:
这里H代表交叉熵, 是一个可调的参数,用来平衡两个交叉熵。我们注意到这个式子的第一项就是一个网络的输出和标签之间传统的交叉熵,而第二项则强制学生网络从教师网络的‘软’输出中学习。
所以说,KD的设计使学生网络模仿教师网络架构,所以有类似的深度。尽管当学生网络的结构稍深一些时,我们发现了KD框架来达到令人鼓舞的效果。但随着我们增加学生网络的深度,KD训练仍然面临着优化深层网络的困难。
3、基于Hint的训练
为了训练很深的FitNet,也就是学生网络(比教师网络更深),我们从教师网络中引入hints的概念。hint 定义为教师网络隐藏层的输出,作用是指导学生网络的学习过程。类似地,我们选择了一个隐藏的FitNet层,即被引导层(the guided layer),从老师的提示层中学习。我们希望被引导层能够预测提示层的输出。注意,有提示是正则化的一种形式,因此,必须选择一对hint/被引导层,这样学生网络就不会过度调整。我们越深入地设置被引导层,我们给网络的灵活性就越小,因此,fitnets就越有可能受到过度调整的影响。在我们的例子中,我们选择hint为教师网络的中间层。类似地,我们选择学生网络的中间层作为被引导层。
考虑到教师网络通常比FitNet更宽,选择的提示层可能比被引导层有更多的输出。出于这个原因,我们向被引导层添加一个回归,它的输出与提示层的大小匹配。然后,我们将训练从第一层到被引导层的FitNet参数,以及回归的参数,通过最小化以下损失函数:
这里uh和vg是老师/学生网络的深度嵌套函数,它们取决于各自提示/被引导层的参数WH/WG,r是Wr参数下最顶端被引导层的回归函数。注意到uh和r的输出必须是可比较的,也就是说uh和r必须是同样非线性的。
尽管如此,使用一个完全连接的回归模型,在被引导和提示层是卷积的情况下,还是会显著增加参数的数量和内存消耗。令N
h,1
*
N
h,2、
O
h
分别表示教师网络提示层的空间大小和通道数量。相似的,让
N
g,1
*
N
g,2、
O
g
为FitNet被引导层的空间大小和通道数量。在一个完全连接的回归矩阵的权重矩阵中,参数的个数是
N
h,1
*
N
h,2
*
O
h
*
N
g,1
*
N
g,2
*
O
g。
为了减少参数数量,我们使用了一个卷积的回归。
设计
卷积的回归使它与教师网络的提示层输入图像的空间区域大致相同。因此,“回归”的输出与教师的hint有相同的空间大小。
给定一个教师网络的提示层,大小
N
h,1
*
N
h,2,回归函数使用了学生网络被引导层输出的大小
N
g,1
*
N
g,2,同时通过一个式子调整内核的形状k1*k2:N
g,i
-k
i
+1=N
h,i
,这样,参数数量为k1*k2*O
h
*O
g ,
显然比之前少得多。
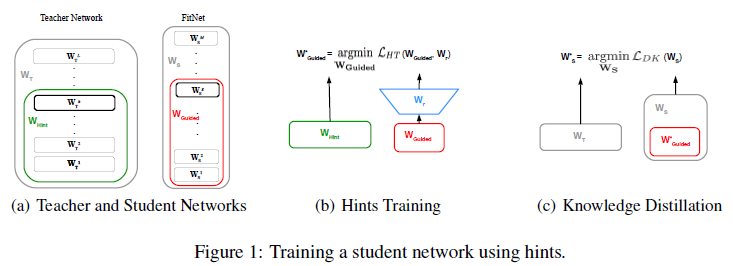
最后,一张图概括一下训练过程。