原理部分:
原理部分参考:
https://blog.csdn.net/yuyuntan/article/details/80141392
霍夫变换公式:
r=xcosθ+ysinθ(x,y代表目标点)
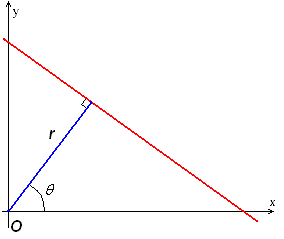
这样图像中的每条直线就对应着一对
。
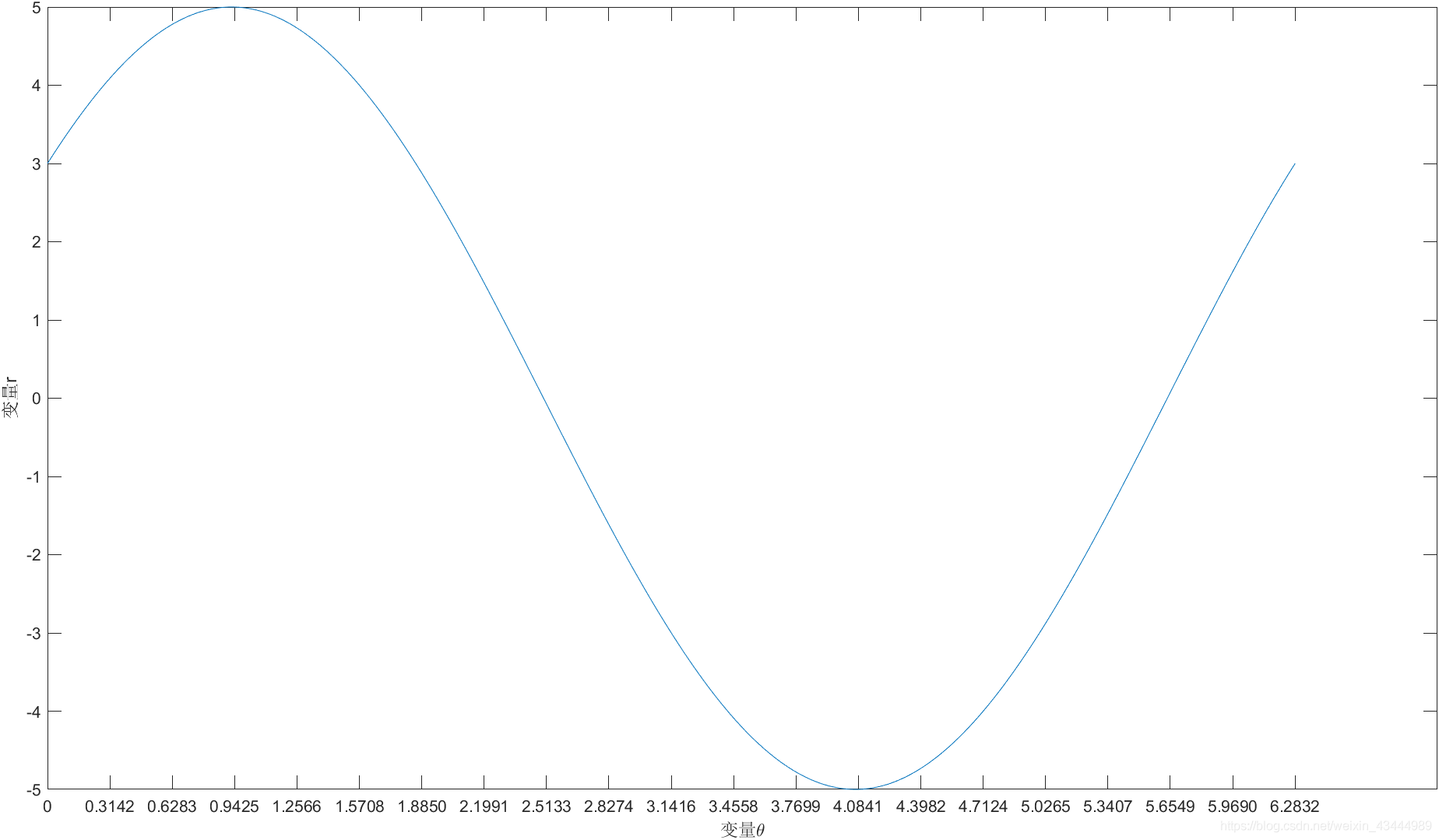
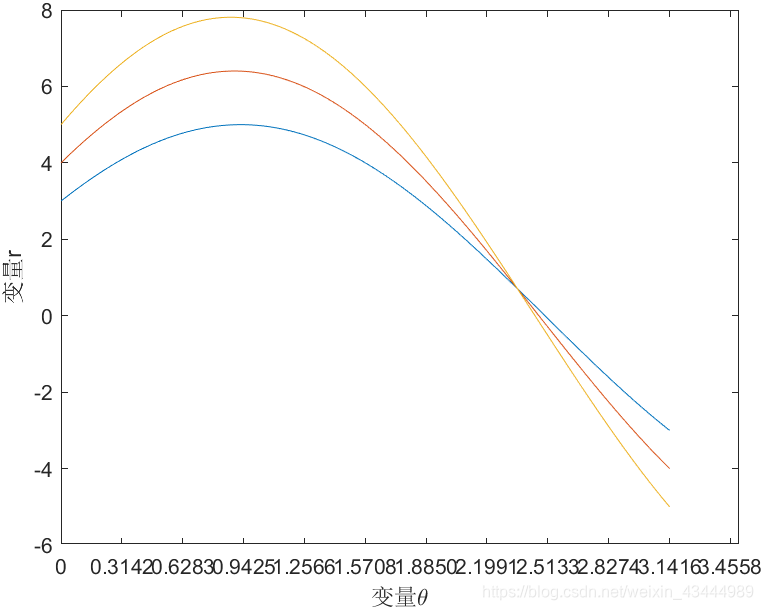
在霍夫空间中一个点映射一条直线,下面的曲线是
过点(3,4)的所有直线的集合
(横轴r,纵轴θ):
所以在霍夫空间检测共线点的问题可以转化为找到并发曲线的问题(即找曲线们霍夫空间中的交点)。
在二维平面坐标系中三个点的霍夫空间参数:
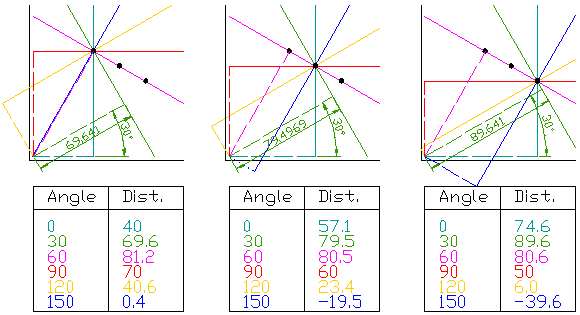
在霍夫空间中这三个位于一条直线的点意味着三条曲线的交点
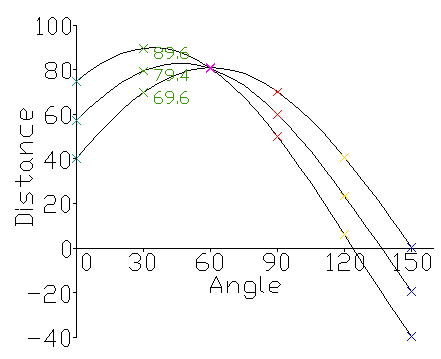
(2,3)(3,4)(4,5):
之于openMV
实现图像二值化和直线拟合显示:
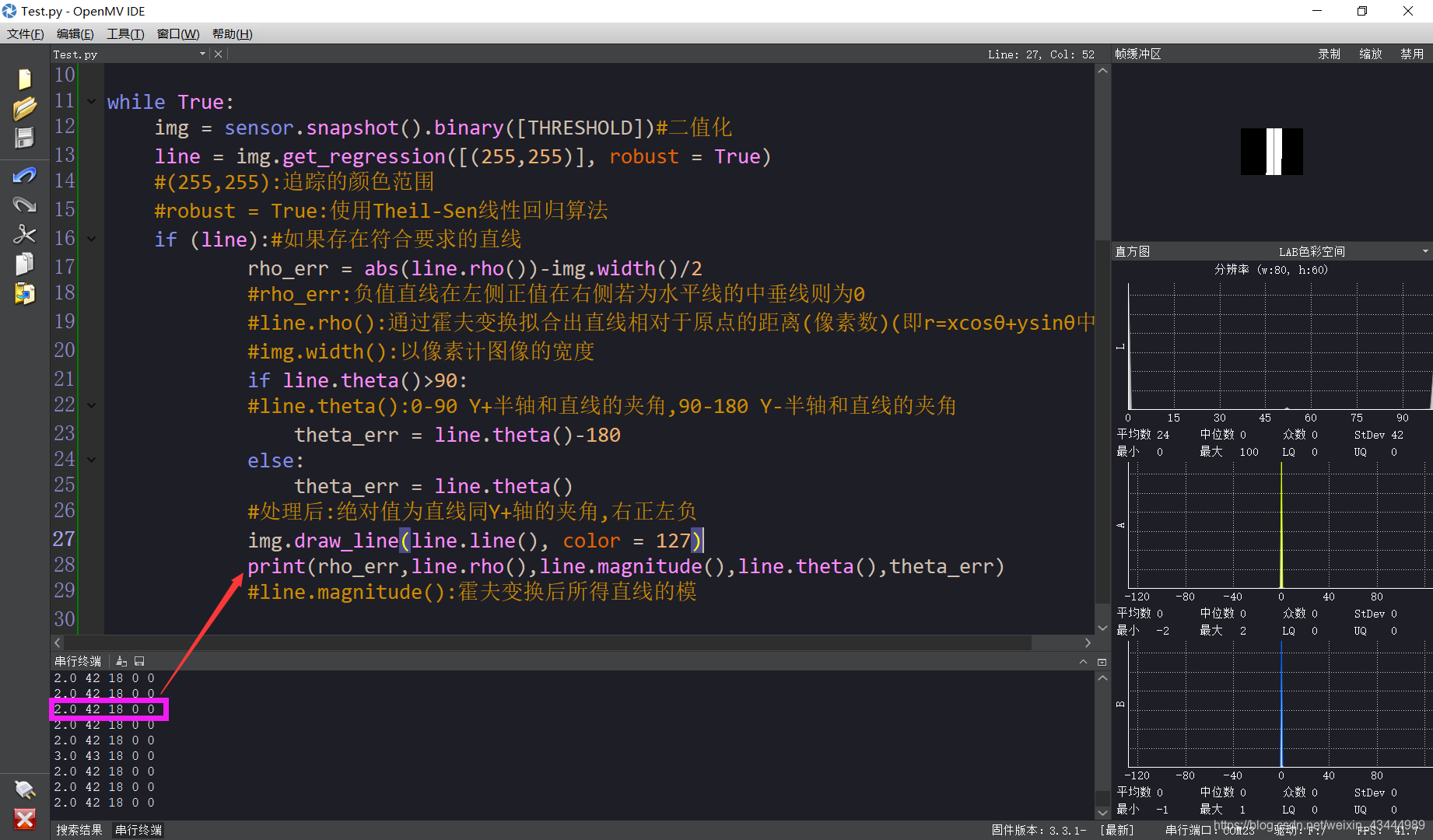
import sensor, image, time
sensor.reset()
sensor.set_pixformat(sensor.GRAYSCALE)
sensor.set_framesize(sensor.QQQVGA)
sensor.skip_frames(time = 3000)
sensor.set_auto_gain(False)
sensor.set_auto_whitebal(False)
clock = time.clock()
THRESHOLD = (0, 110)#二值化阈值(灰度)
while True:
img = sensor.snapshot().binary([THRESHOLD])#二值化
line = img.get_regression([(255,255)], robust = True)
#(255,255):追踪的颜色范围
#robust = True:使用Theil-Sen线性回归算法
if (line):#如果存在符合要求的直线
rho_err = abs(line.rho())-img.width()/2
#rho_err:负值直线在左侧正值在右侧若为水平线的中垂线则为0
#line.rho():通过霍夫变换拟合出直线相对于原点的距离(像素数)(即r=xcosθ+ysinθ中的r)
#img.width():以像素计图像的宽度
if line.theta()>90:
#line.theta():0-90 Y+半轴和直线的夹角,90-180 Y-半轴和直线的夹角
theta_err = line.theta()-180
else:
theta_err = line.theta()
#处理后:绝对值为直线同Y+轴的夹角,右正左负
img.draw_line(line.line(), color = 127)
print(rho_err,line.rho(),line.magnitude(),line.theta(),theta_err)
#line.magnitude():霍夫变换后所得直线的模