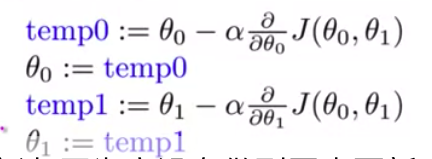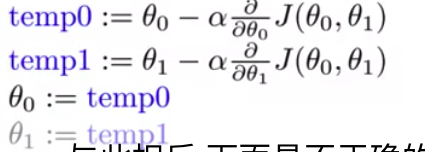线性回归
回归就是输出是连续的函数,那么线性回归就是输出是直线的连续函数。也就是我们数学中所说的一次函数。
Y = θ1X+θ0
在这个函数里有两个参数:θ1和θ0。θ1是斜率,θ2是截距。想下边这个房价与面积关系图片

我们会在大脑中把这些点组合起来,大致是一条过原点的直线,则可以写为
Y = 0.8X
对应到线性回归公式中,θ1为0.8,θ0为0。
那怎么判断这个回归是否准确?则要引入另一个函数:
损失函数

它的意思是,真实值与预测值差的平方的均值除以二。
当损失函数的值越小,我们的线性回归也就越准确。在公式中不太好判断什么时候较小,我们拿一个例子说一下:

左边是x、y的原始数据图像,我们可以拟合一个回归函数来反应x与y之间的关系;右边是损失函数与θ1的关系函数。在右边图像中就可以非常直观的反应损失函数与线性回归是否足够正确拟合图像。
-
y = x
在原始数据中,有三个点(1,1)、(2,2)、(3,3)。这三个点正好都在y=x这条直线上。所以通过损失函数公式计算下J=0 -
y = 0.5x
j = [(0.5
1-1)
2
+(0.5
2-2)
2
+(0.5
3-3)
2
]/(2
3) -
y = 0
x
j = [(0
1-1)
2
+(0
2-2)
2
+(0
3-3)
2
]/(2
3)
可以得到这样的一条抛物线

在这个图上可以很明显看出当θ1=0.5时,损失函数有最小值。随着θ1增大或者见效,损失之都会增加。这样我们就能很清晰看出损失函数与θ1、θ0之间的关系。
一个参数
,我们用
二维
表示出来了损失函数;那么
两个参数
是否就是用
三维*来表示呢?

确实如此,这是
Y = θ1X+θ0
生成的损失值图像,但是这种立体的不是太直观,我们不能具体看出θ1、θ0分别是多少时有相应的J。所以我们进行降维处理,得到轮廓图:

轮廓图就像是初高中地理的等高线图,中心的谷底,在这里呢就是J取得最小值。
怎样快速到达谷底呢?就得沿着最陡的地方下降。对应的呢就是沿着梯度的方向下降,我们可以最快得到最小的损失值。
梯度下降

这个图上可以看出,在不同山峰(红的)会降到不同的谷底(蓝色)这正是梯度下降的一个特点:
1:参数取不同的初始值,可能会得到不同的最小损失值。但这资额不同的损失值却不能说谁不对,因为他们分别是此模型的局部最优解,就像你身处谷底就不可能知道还有更低的地方
公式是:

第二个特点呢是:
多个参数时,需同步更新,像这样:
而不是这样