目录
序言
kafka在0.11版本后提供了
Range、Round Robin、Sticky
三种consumer group partition分配策略,其中Range、Round Robin比较简单,Sticky有些复杂,但Sticky的平衡效果最好。有点需要注意,consumer group partition分配策略是在consumer端完成分配计划后发送给GroupCoordiantor,最后由GroupCoordinator传播给其它consumer。这种设计有两个优点,consumer完成分配计划,减少了GroupCoordinator的压力,增加了GroupCoordinator灵活性。由GroupCoordinator传播给其它Consumer,避免了consumer之间互联。(
注意:
本文说的消费均衡是
参与消费
的单个Consumer消费Partition数量均衡,不是指consumer group 中所有的Consumer进程之间的消费均衡
)
Range
Range策略是针对单个Topic设计的。如果Consumer Group只订阅了单个Topic,那么消费会很均衡。不论怎么Rebalance,参与消费的consumer之间的partition数量之差最多为1,理想情况下可以达到0,我们称这个为
平衡分数
(这个概念下面也会用到)。平衡分数越接近0平衡性越好,0是最完美的。如果Consumer Group订阅了多个Topic,平衡分数比较大,订阅的Topic越多,平衡分数越大,平衡效果越差,不建议Range策略使用在此场景下。
算法
//单个Topic的partition数量除以consumer数量,得每个consumer可得partition数量
int numPartitionsPerConsumer = numPartitionsForTopic / consumersForTopic.size();
//单个Topic的partition数量模consumer数量,得余数
int consumersWithExtraPartition = numPartitionsForTopic % consumersForTopic.size();
List<TopicPartition> partitions = AbstractPartitionAssignor.partitions(topic, numPartitionsForTopic);
for (int i = 0, n = consumersForTopic.size(); i < n; i++) {
//partition按区间分配给consumer
int start = numPartitionsPerConsumer * i + Math.min(i, consumersWithExtraPartition);
//加上余数,加完为止
int length = numPartitionsPerConsumer + (i + 1 > consumersWithExtraPartition ? 0 : 1);
assignment.get(consumersForTopic.get(i)).addAll(partitions.subList(start, start + length));
}
示例
1、consumer group 有三个consumer,分别为C={C0、C1、C2},消费Topic T 有5个partition P={p0,p1,p2,p3,p4}
首初分配结果:
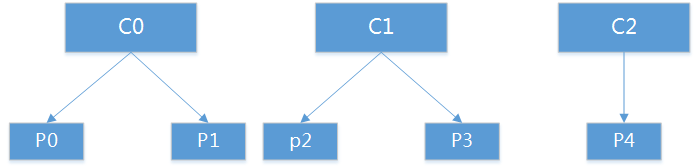
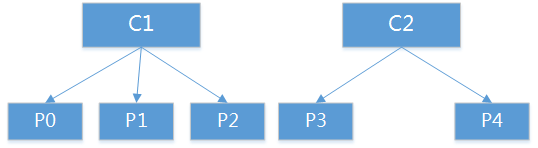
consumer数量不变与上面一致。如果C0掉线,分配结果如下:
2、consumer group 有三个consumer,分别为C={C0、C1、C2},消费Topic t0有5个partition P={p0,p1,p2,p3,p4},T1有4个partition P={p0,p1,p2,p3}
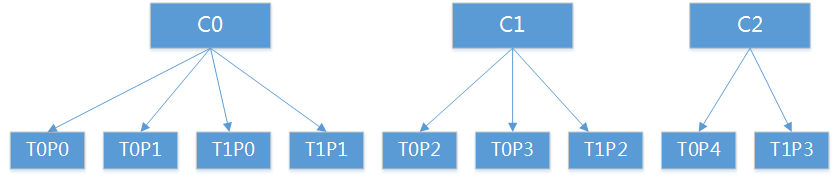
从上图可以看出,consumer group 消费多Topic会出现不均衡,随着Topic变多,均衡性越差。
Round Robin
Round Robin策略在设计中考虑了同一个Consumer Group消费多个Topic,因此消费多个Topic会表现的比较好的平衡性。同时也具有Range策略的优势。但Consumer Group中各自consumer订阅的Topic不同时Round Robin平衡性表现会比较差。
算法
1、基于字符顺序构建有序consumer集合列表,基于取模特性,达到一个
首尾相连有序环
效果

2、基于Topic字符顺序构建有序partition集合列表
3、遍历有序partition集合,从有序环中取出consumer,并分配给partition
核心源码
基于有序列表,达到首尾相连有序环的效果
@Override
public T next() {
T next = list.get(i);
//基于取模特性,下标介于[0,list.size-1]之间
i = (i + 1) % list.size();
return next;
}
示例
1、consumer group 有三个consumer,分别为C={C0、C1、C2},消费Topic t0有5个partition P={p0,p1,p2,p3,p4},T1有4个partition P={p0,p1,p2,p3}

2、consumer group 有三个consumer,分别为C={C0、C1、C2}。3个Topic,分别为T0的P={T0P0},T1的P={T0P0,T1P1},T2的P={T2P0,T2P1,P2P2}。 其中C0订阅了T0、T1,C1订阅了T0、T1,C2订阅了T1、T2。即同一个consumer group下所有consumer订阅的topic不同,这种情况下平衡性表现不理想。
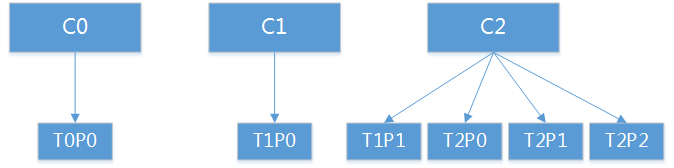
Sticky
Sticky策略是我们今天重点要讲的,Sticky不具有Range、Round Robin两种策略的缺陷,在单Topic、多Topic、consumer group中Consumer订阅的Topic不同等复杂情况下都有良好的平衡性。Sticky策略的源码有些复杂,初看会觉的杂乱无序,而且注释不多,但多看几遍发现代码逻辑挺清晰。
数据结构&算法
数据结构
Sticky策略没有一个专门的数据结构,而是一个核心数据结构和多个辅助结构。采用Map<String,List<TopicPartition>>结构做为核心数据结构,记录分配情况,Key为consumer,Value为consumer分配的partition集合。如图:
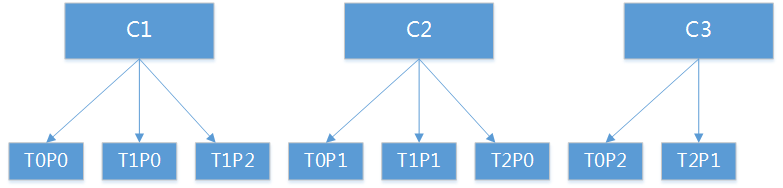
要做到上面的分配效果需要几个辅助集合:
1、有序consumer TreeSet集合,以consumer当前分配的partition数量做升序
2、有序可分配的partition List集合,基于consumer顺序,同一个consumer中以partition下标做升序
3、partition可被分配的consumer Map集合,key:partition,value:可分配的consumer集合
4、consumer可订阅的partition Map集合,key:consumer,vlaue:可订阅的partition集合
注意:第三个集合大于或者等于第四个集合,因为第三个集合从Topic视角组装集合
算法
算法逻辑上有几个难点:
一、判断平衡性
1、每个consumer被分配的partition数量相等或者差异为1,那么已经是很理想的平衡分数。
二、partition是否需要重新分配Consumer
为方便说明记:
partition当前consumer订阅的partition数量为
current.p.count
partition上个consumer订阅的partition数量为
prev.p.count
partition可分配的consumer订阅的partition数量为
potential.p.count
1、检查partition是否发生了generation冲突且
current.p.count>prev.p.count+1
,需要重新分配Consumer。
2、检查
current.p.count>potential.p+1或者current.p.count+1<potential.p
,需要重新分配Consumer
(备注:这里需要注意下,在源码里面没有current.p.count+1<potential.p判断,这是源码巧妙的地方,在performReassignments方法中只有达到平衡后才会退出,在partitions为基础的死循环的过程中current和potential的视角是不断变化的。例如:p0时,c1是current consumer,但在p1时,c1是potential consumer,所以源码只做单方向判断。)
三、粘性处理
粘性处理是Sticky策略最亮眼的地方,在保证最大可能的平衡的情况下,确保partition—>consumer的变化最少。
在粘性处理准则与最大可能平衡平衡准则有冲突,以最大可能平衡优先。
逻辑:
1、构建分配策略的时候,优先保持原有的分配
2、记录Partition最近一 次的移动轨迹,移动轨迹通过src—->dst表示。
假设T0P0最近一次的移动轨迹为C1—->C2,本次计划从C2—->C1(称为反转),存在C2—>C1移动记录,不允许这样移动。从Partition的Topic移动轨迹中找一个移动轨迹一样的Partition出来进行分配。
假设T0P0最近一次的移动轨迹为C1—->C2,本次计划从C2—->C3,反转后变为C3—->C1,不存C3—->C1移动记录,可以移动。
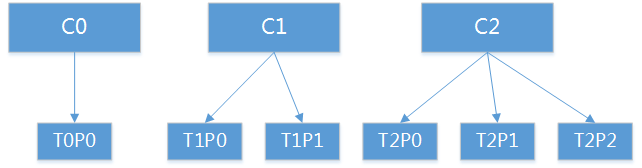
示例
1、consumer group 有三个consumer,分别为C={C0、C1、C2}。3个Topic,分别为T0的P={T0P0},T1的P={T0P0,T1P1},T2的P={T2P0,T2P1,P2P2}。 其中C0订阅了T0、T1,C1订阅了T0、T1,C2订阅了T1、T2。
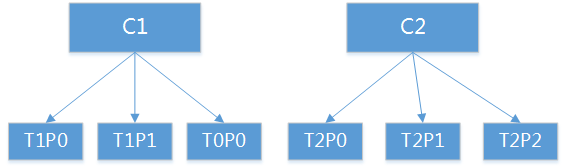
如果C0被删除,分配如下
核心方法
代码步骤
1、构建当前的分配情况
currentAssignment是基于上次订阅情况构建,结构key:consumer, value:list<partition>,构建过程中有generation冲突的consumer,取generation最大的consumer
2、构建可能的分配组合
从partition角度看,构建partition2AllPotentialConsumers
从consumer角度看,构建consumer2AllPotentialPartitions
3、排序partitions
对所有合法的partition进行排序,确保重分配阶段partition在consumer之间移动最小
排序原则:即订阅partition量最多的cosumer涉及的partition排在前面,因为这些partition最有可能需要重分配
a. 重平衡且partition2AllPotentialConsumers中值均相等且consumer2AllPotentialPartitions中值均相等
b.
//重分配且P与C呈倍数关系,需要进行sort partition操作
// 操作CurrentAssignment
// 1、过滤掉不存在的Partition集合
// 2、产生Generation冲突的Partition集合与每个Consumer的Partitions做交集处理
// loop
// a. 存在交集:取交集中一个partition
// b. 不存在交集:取Consumer订阅的一个partition
// end loop
// 3、添加没有被订阅的partition
//按照可订阅Partition的consumer数量做升序排序,并以此顺序转换为List集合
4、平衡处理
a. 分配未分配的partition
遍历sortedCurrentSubscriptions,按顺序分配可分配的consumer,并对sortedCurrentSubscriptions重新排序
缩小重新分配的范围
b.过滤掉不需要重新分配的partition和consumer
1、缩小到那些需要重新分配的partition
寻找真正可以被重新分配的partition,一个partition可选择的consumer小于2,说明是不可以重新分配
2、缩小到那些需要重新分配的consumer
a. consumer已经订阅的p的数量小于可订阅的p的数量,说明consumer是可重新分配的
b. 一个partition可选择的consumer大于等待2,说明consumer是可重新分配的
c. 不符合a、b两个条件的consumer为不可重新分配的
c.执行重分配
1、遍历有序partition
2、检查当前的分配策略是否均衡,检查consumer订阅的partition的数量
a. 有序的consumer集合,比较first consumer与last consumer订阅的partition数量,如果两者相等或者差一,说明已经平衡
b. 比较订阅了同一个主题的两个consumer所分配的partition数量之差
(可订阅但没有订阅的partition所对应的consumer订阅的情况)
consumer可订阅的partition集合L,consumer当前订阅的partition集合M,
遍历集合L,判断L1是否在集合M中,若不在查看p当前的消费者c2,
判断c1.count<c2.count(这里的count指订阅的所有topic),说明不均衡
3、检查partition是否需要重新分配
a. 检查partition是否属于generation冲突且current consumer的partition数量大于prev consumer的partition.size+1,
说明需要重新分配
b. 检查partition可选择的consumer订阅的partition数量加1小于当前consumer订阅的partition数量
4、遍历有序consumer(优先找订阅少的consumer)寻找一个可订阅当前partition的consumer并分配给它
5、粘性分配
a. 记录每次分配或者partition迁移
b.如果partition有迁移记录,C1—>C2且C2—–>C1,那么改变分配的partition
6、对比两次分配的平衡效果。消费者订阅partition数量的差异之和为平衡分数,平衡分数越接近0越平衡。
平衡判断
private boolean isBalanced(Map<String, List<TopicPartition>> currentAssignment,
TreeSet<String> sortedCurrentSubscriptions,
Map<String, List<TopicPartition>> allSubscriptions) {
//有序consumer的首尾元素的partition数量差异
int min = currentAssignment.get(sortedCurrentSubscriptions.first()).size();
int max = currentAssignment.get(sortedCurrentSubscriptions.last()).size();
//符合条件说明已经很平衡了
if (min >= max - 1)
return true;
// create a mapping from partitions to the consumer assigned to them
final Map<TopicPartition, String> allPartitions = new HashMap<>();
Set<Entry<String, List<TopicPartition>>> assignments = currentAssignment.entrySet();
for (Map.Entry<String, List<TopicPartition>> entry: assignments) {
List<TopicPartition> topicPartitions = entry.getValue();
for (TopicPartition topicPartition: topicPartitions) {
if (allPartitions.containsKey(topicPartition))
log.error("{} is assigned to more than one consumer.", topicPartition);
allPartitions.put(topicPartition, entry.getKey());
}
}
// for each consumer that does not have all the topic partitions it can get make sure none of the topic partitions it
// could but did not get cannot be moved to it (because that would break the balance)
for (String consumer: sortedCurrentSubscriptions) {
List<TopicPartition> consumerPartitions = currentAssignment.get(consumer);
int consumerPartitionCount = consumerPartitions.size();
// skip if this consumer already has all the topic partitions it can get
// 满足平衡要求
if (consumerPartitionCount == allSubscriptions.get(consumer).size())
continue;
List<TopicPartition> potentialTopicPartitions = allSubscriptions.get(consumer);
for (TopicPartition topicPartition: potentialTopicPartitions) {
if (!currentAssignment.get(consumer).contains(topicPartition)) {
String otherConsumer = allPartitions.get(topicPartition);
int otherConsumerPartitionCount = currentAssignment.get(otherConsumer).size();
//关联consumer之间比较partition数量,判断平衡要求
if (consumerPartitionCount < otherConsumerPartitionCount) {
return false;
}
}
}
}
return true;
}
执行分配
private boolean performReassignments(List<TopicPartition> reassignablePartitions,
Map<String, List<TopicPartition>> currentAssignment,
Map<TopicPartition, ConsumerGenerationPair> prevAssignment,
TreeSet<String> sortedCurrentSubscriptions,
Map<String, List<TopicPartition>> consumer2AllPotentialPartitions,
Map<TopicPartition, List<String>> partition2AllPotentialConsumers,
Map<TopicPartition, String> currentPartitionConsumer) {
boolean reassignmentPerformed = false;
boolean modified;
// 执重复执行分配直到平衡为止
do {
modified = false;
Iterator<TopicPartition> partitionIterator = reassignablePartitions.iterator();
//判断是否平衡且可分配Partition不为空
while (partitionIterator.hasNext() && !isBalanced(currentAssignment, sortedCurrentSubscriptions, consumer2AllPotentialPartitions)) {
TopicPartition partition = partitionIterator.next();
if (partition2AllPotentialConsumers.get(partition).size() <= 1)
log.error("Expected more than one potential consumer for partition '{}'", partition);
String consumer = currentPartitionConsumer.get(partition);
if (consumer == null)
log.error("Expected partition '{}' to be assigned to a consumer", partition);
//Generation冲突的Partition
if (prevAssignment.containsKey(partition) &&
currentAssignment.get(consumer).size() > currentAssignment.get(prevAssignment.get(partition).consumer).size() + 1) {
reassignPartition(partition, currentAssignment, sortedCurrentSubscriptions, currentPartitionConsumer, prevAssignment.get(partition).consumer);
reassignmentPerformed = true;
modified = true;
continue;
}
//订阅同一个Topic的consumer之间partition数量差异比较,判断partition是否需要分配
for (String otherConsumer: partition2AllPotentialConsumers.get(partition)) {
if (currentAssignment.get(consumer).size() > currentAssignment.get(otherConsumer).size() + 1) {
reassignPartition(partition, currentAssignment, sortedCurrentSubscriptions, currentPartitionConsumer, consumer2AllPotentialPartitions);
reassignmentPerformed = true;
modified = true;
break;
}
}
}
} while (modified);
return reassignmentPerformed;
}