博客

论文中一些软阈值的处理：

软阈值一般是用来解决这种优化问题的情形的，式子中含有L1范数正则化，可以进行稀疏选择和降噪：



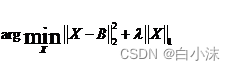
上面软阈值的解为：



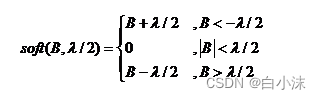
即soft(B, λ/2)

当上面的形式变为：



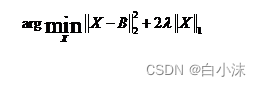
解为soft(B, λ)

其中B为变量，λ为阈值，可见第一项的系数为1的时候，阈值应该取第二项系数的1/2.

可以在Matlab中编写代码来实现：

软阈值函数代码：【通用形式】

function [ x ] = soft( b,T ) 
     x = sign (b).* max ( abs (b) - T,0); 
end 

编写主函数调用soft(B, λ/2)

clear all ; close all ; clc ;  
b = [-0.8487   -0.3349    0.5528    1.0391   -1.1176]'; 
lambda = 1; 
x1=soft(b,lambda) 

在matlab中绘制软阈值的图像：

x=-5:0.1:5;T=1;y=soft(x,T); plot (x,y); grid ; 

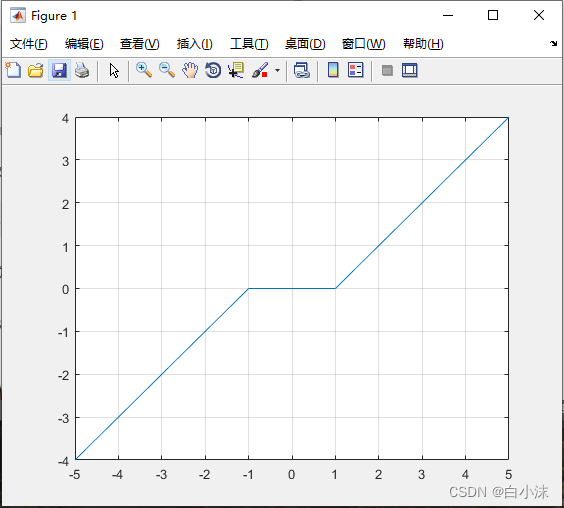
实际应用-论文中出现的一些软阈值的优化处理

参考文章：

1.https://blog.csdn.net/h_l_dou/article/details/83718034这篇文章说的非常详细！】

2.Cai J, Cand˙es EJ, Shen Z (2010) A singular value thresholding algorithm for matrix completion. SIAM J Optim 20(4):1956–1982

3.[Donoho, 1995] David L Donoho. De-noising by softthresholding. TIT, 41(3):613–627, 1995