Transformer总结和梳理
首先来看一下Transformer结构的结构:
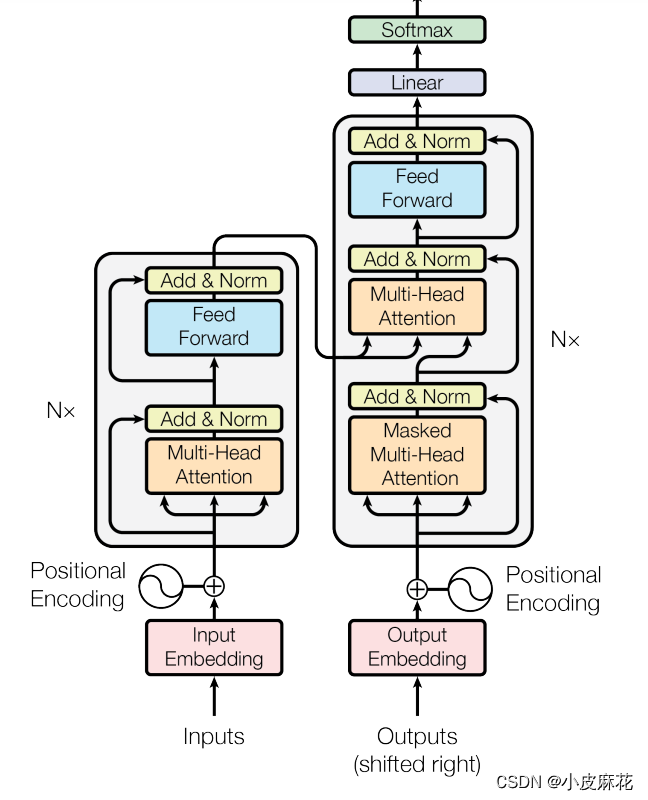
Transformer是由Encoder和Decoder两大部分组成,首先我们先来回顾一下Transformer的结构:Transformer结构主要分为两大部分,一是Encoder层结构,另一个则是Decoder层结构。
Encoder 的输入由 Input Embedding 和 Positional Embedding 求和输入Multi-Head-Attention,然后又做了一个ADD&Norm,再通过Feed Forward进行输出,最后又做了一个ADD&Norm,这就是Decoder。
Decoder和Encoder有很多相同的地方,Decoder首先也是需要进行 Input Embedding 和 Positional Embedding 求作为输入,并且Decoder中的第一个Attention模块为Mask Attention,还有一个就是Decoder的K和V分别均来自Encoder。
接下来看一下每个模块的具体理解:
Positional encoding
首先对于文本特征,需要进行Embedding,由于transformer抛弃了Rnn的结构,不能捕捉到序列的信息,交换单词位置,得到相应的attention也会发生交换,并不会发生数值上的改变,所以要对input进行Positional Encoding。
Positional encoding和input embedding是同等维度的,所以可以将两者进行相加,的到输入向量
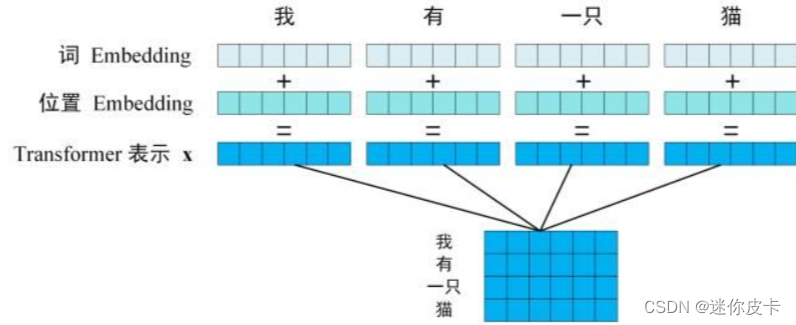
接下来看一些Positional Encoding的计算公式:
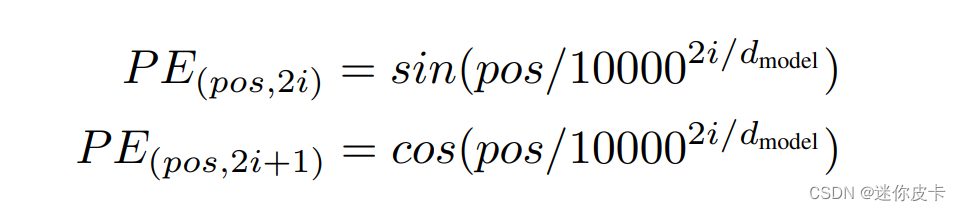
其中pos表示token在sequence中的位置,d_model表示词嵌入的维度,i则是range(d_model)中的数值,也就是说:对于单个token的d_model维度的词向量,奇数位置取cos,偶数位置取sin,最终的到一个维度和word embedding维度一样的矩阵,接下来可以看一下代码:
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
def get_positional_encoding(max_seq_len, embed_dim):
# 初始化一个positional encoding
# embed_dim: 字嵌入的维度
# max_seq_len: 最大的序列长度
positional_encoding = np.array([
[pos / np.power(10000, 2 * i / embed_dim) for i in range(embed_dim)] if pos != 0 else np.zeros(embed_dim) for pos in range(max_seq_len)])
positional_encoding[1:, 0::2] = np.sin(positional_encoding[1:, 0::2]) # dim 2i 偶数
positional_encoding[1:, 1::2] = np.cos(positional_encoding[1:, 1::2]) # dim 2i+1 奇数
return positional_encoding
positional_encoding = get_positional_encoding(max_seq_len=100, embed_dim=16)
plt.figure(figsize=(10, 10))
sns.heatmap(positional_encoding)
plt.title("Sinusoidal Function")
plt.xlabel("hidden dimension")
plt.ylabel("sequence length")
plt.show()
首先求初始向量:positional_encoding,然后对其奇数列求sin,偶数列求cos:
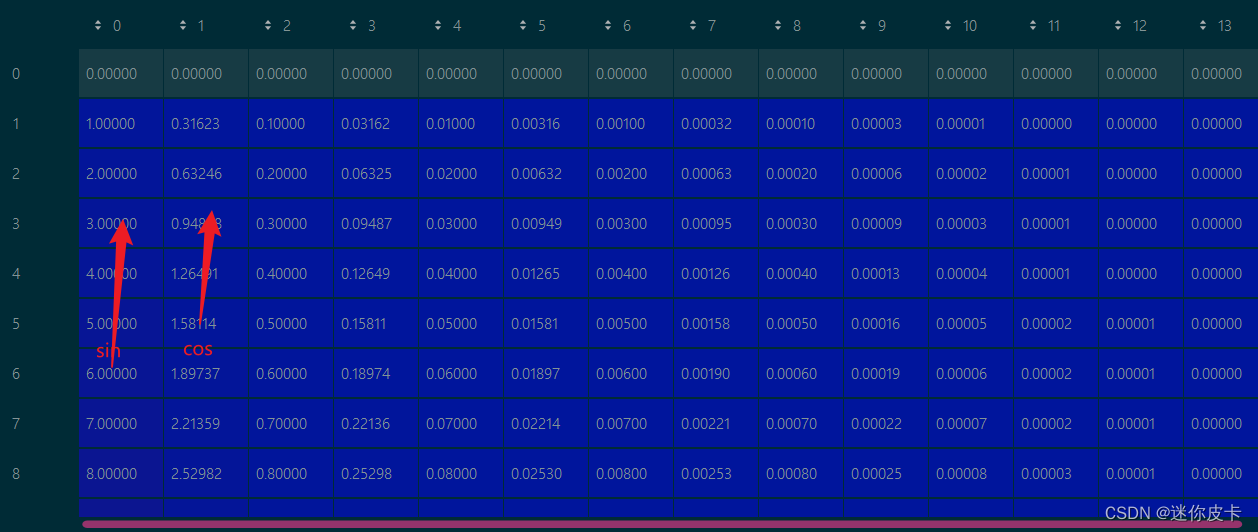
最终得到positional encoding之后的数据可视化:
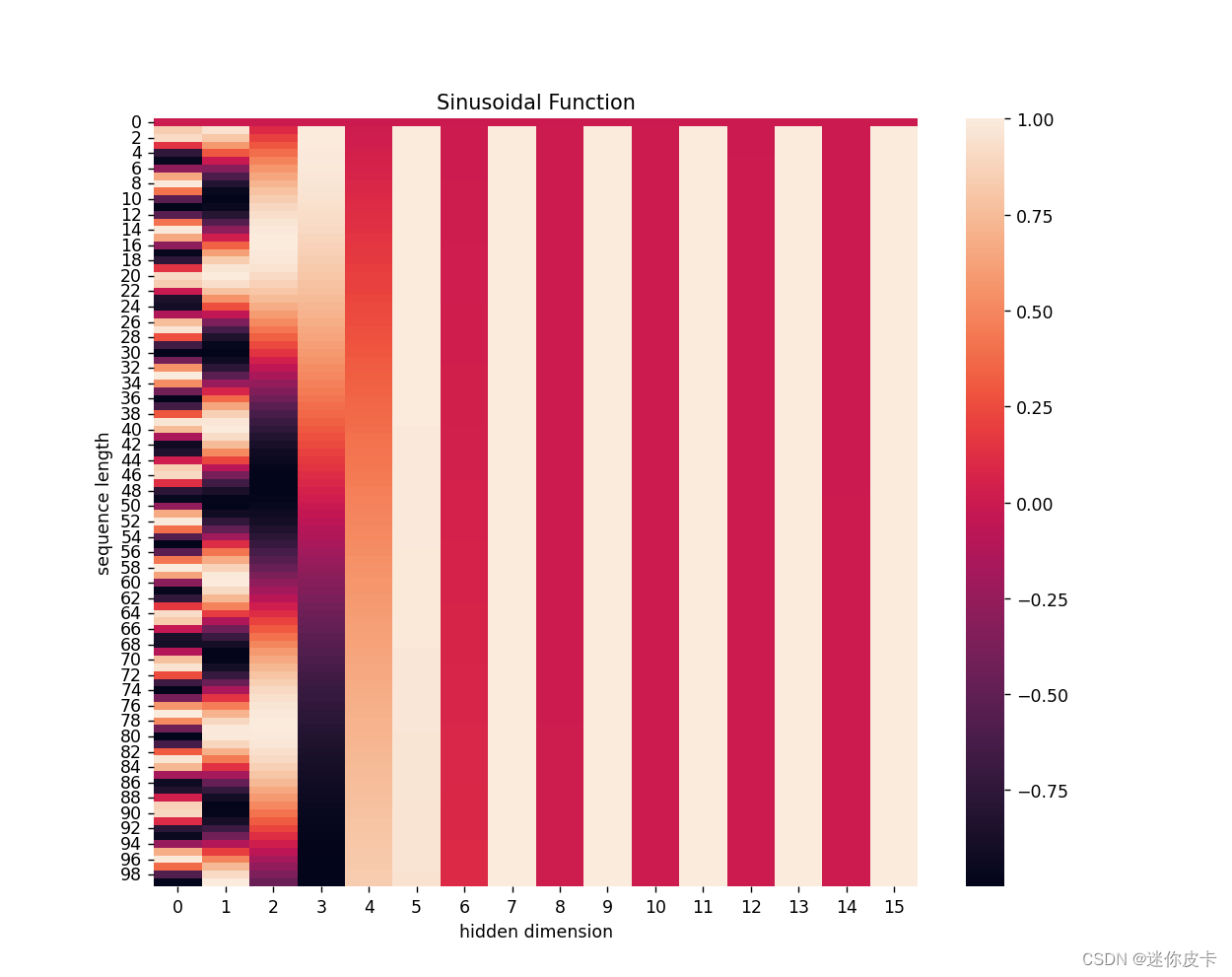
Self-attention
何为self-attention?首先我们要明白什么是attention,对于传统的seq2seq任务,例如中-英文翻译,输入中文,得到英文,即source是中文句子(x1 x2 x3),英文句子是target(y1 y2 y3)
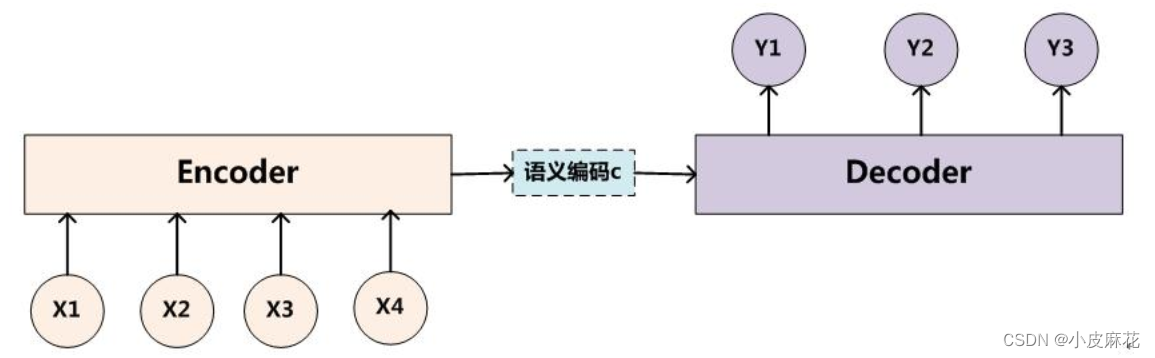
attention机制发生在target的元素和source中的所有元素之间。简单的将就是attention机制中的权重计算需要target参与,即在上述Encoder-Decoder模型中,Encoder和Decoder两部分都需要参与运算。
而对于self-attention,它不需要Decoder的参与,而是source内部元素之间发生的运算,对于输入向量X,对其做线性变换,分别得到Q、K、V矩阵
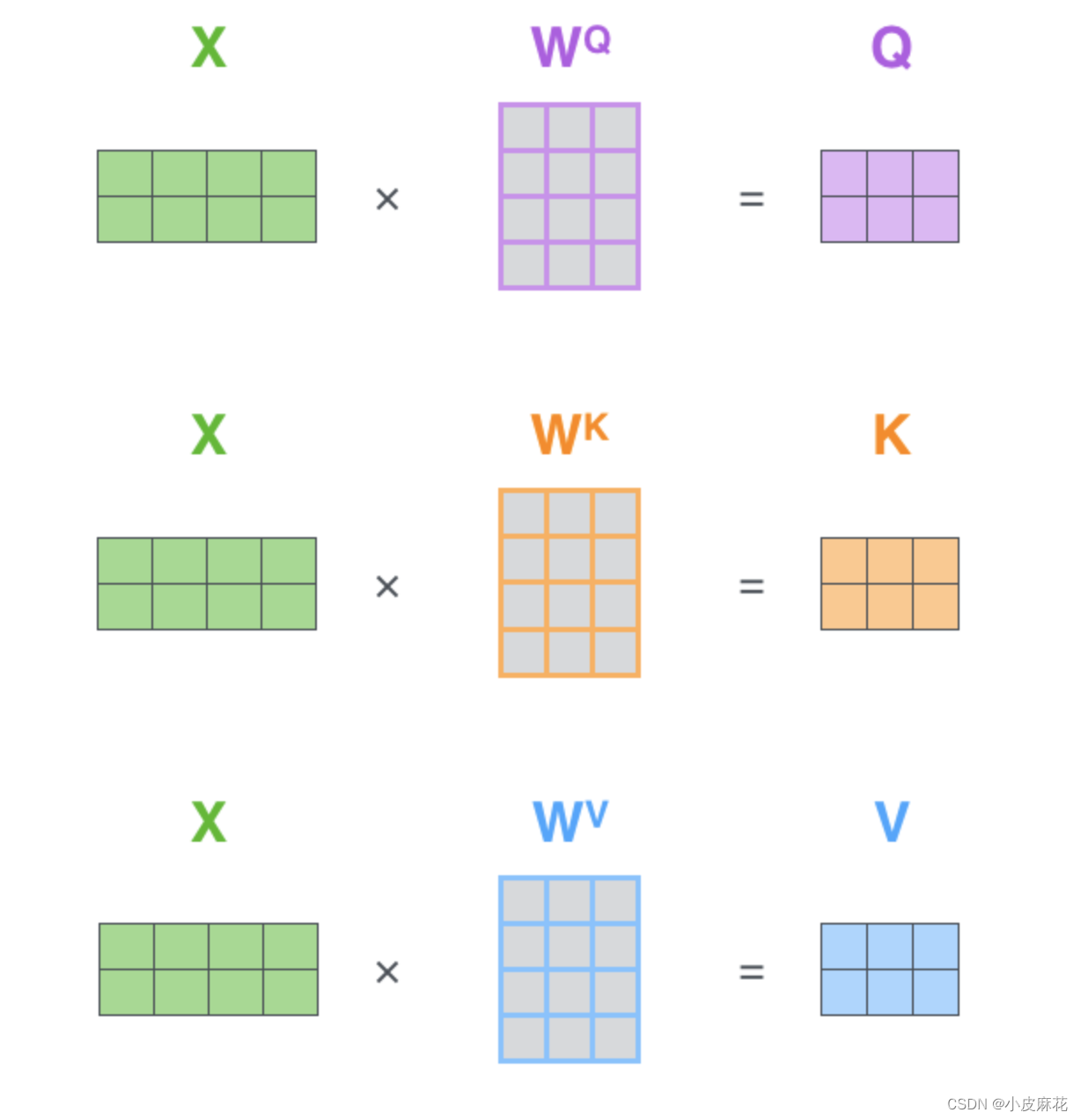
然后去计算attention,Q、K点乘得到初步的权重因子,并对Q、K点乘结果进行放缩,除以sqrt(dk),Q、K点乘之后的方差会随着维度的增大而增大,而大的方差会导致极小的梯度,为了防止梯度消失,所以除以sqrt(dk)来减小方差,最终再加一个softmax就得到了self attention的输出。
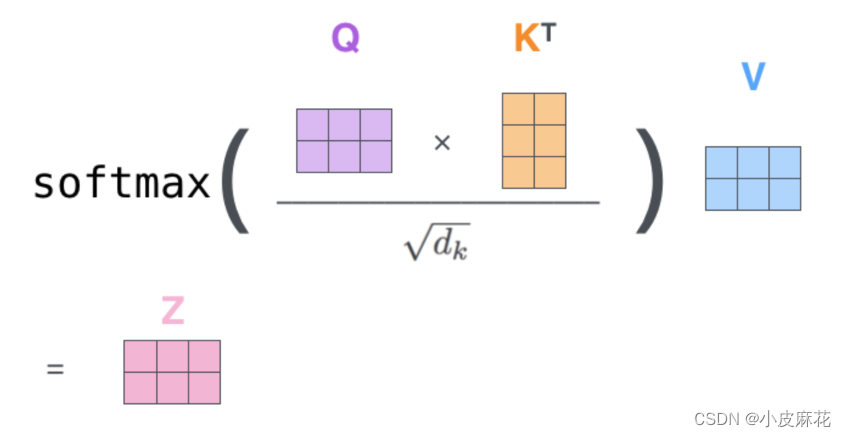
Multi–head-attention
Multi–head-attention使用了多个头进行运算,捕捉到了更多的信息,多头的数量用h表示,一般h=8,表示8个头
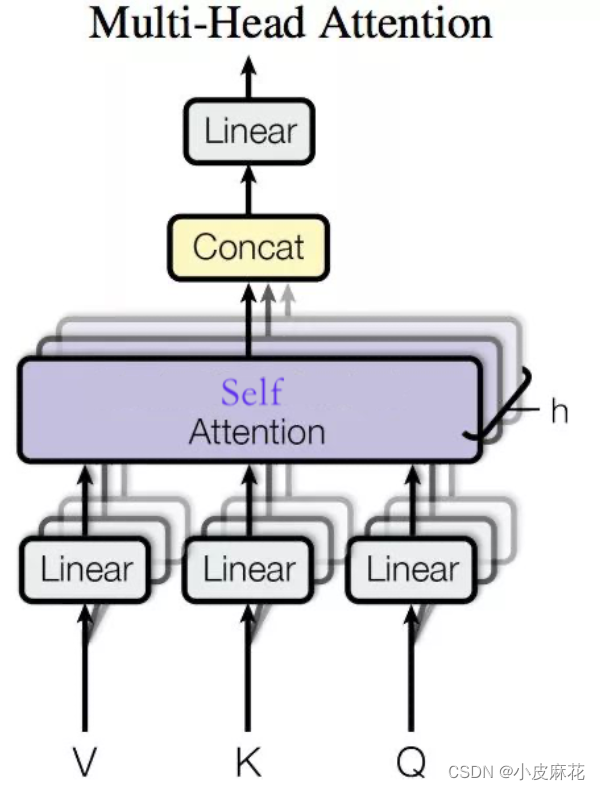
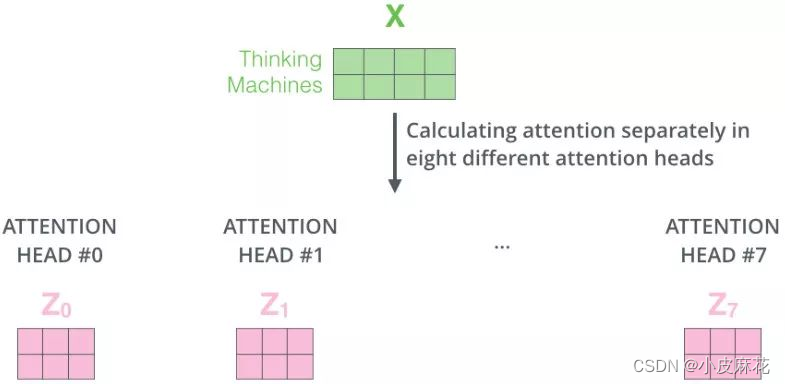
在输入每个self-attention之前,我们需将输入X均分的分到h个头中,得到Z1-Z7八个头的输出结果。
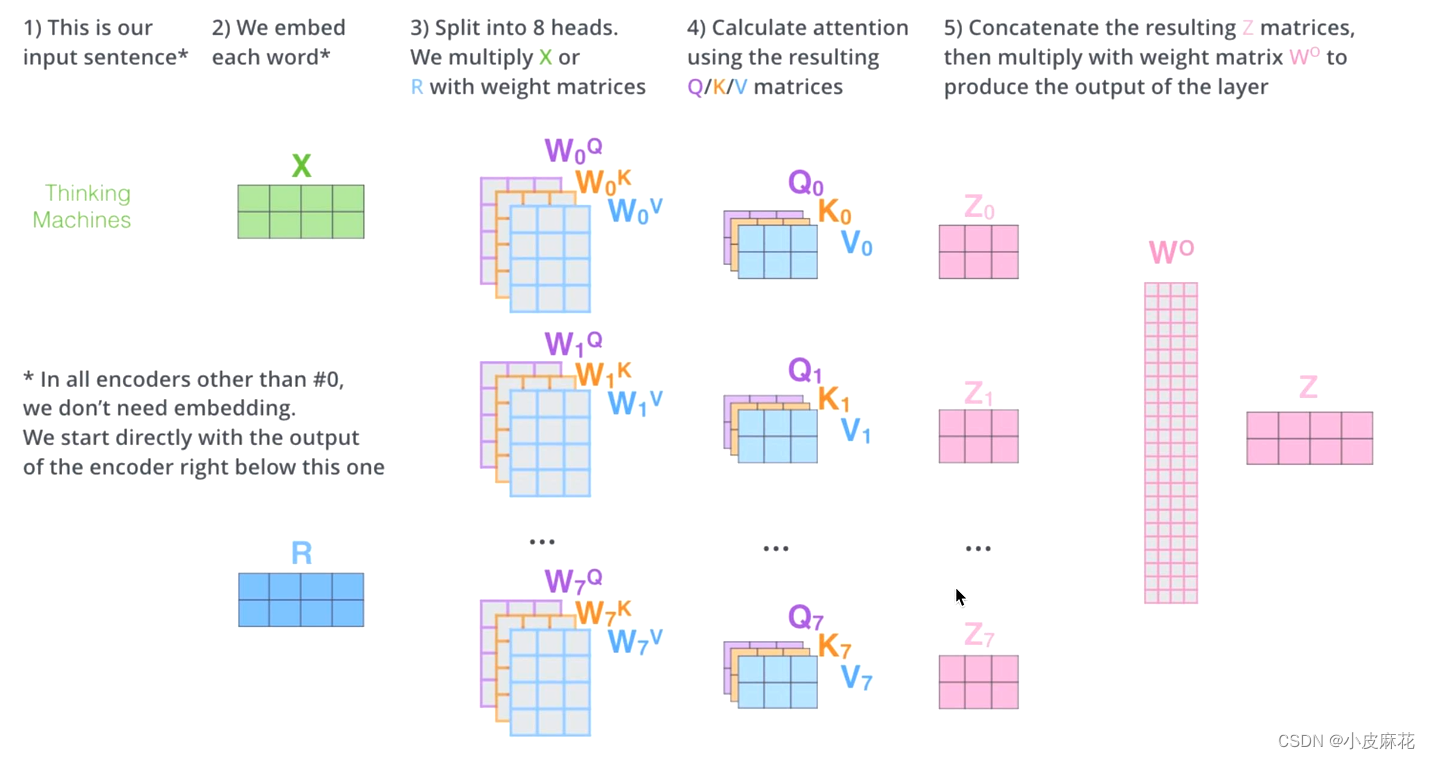
对于每个头计算相应的attention score,将其进行拼接,再与W0进行一个线性变换,就得到最终输出的Z。
Add&Norm
Add操作
首先我们还是先来回顾一下Transformer的结构:Transformer结构主要分为两大部分,一是Encoder层结构,另一个则是Decoder层结构,Encoder 的输入由 Input Embedding 和 Positional Embedding 求和输入Multi-Head-Attention,再通过Feed Forward进行输出。
由下图可以看出:在Encoder层和Decoder层中都用到了Add&Norm操作,即残差连接和层归一化操作。
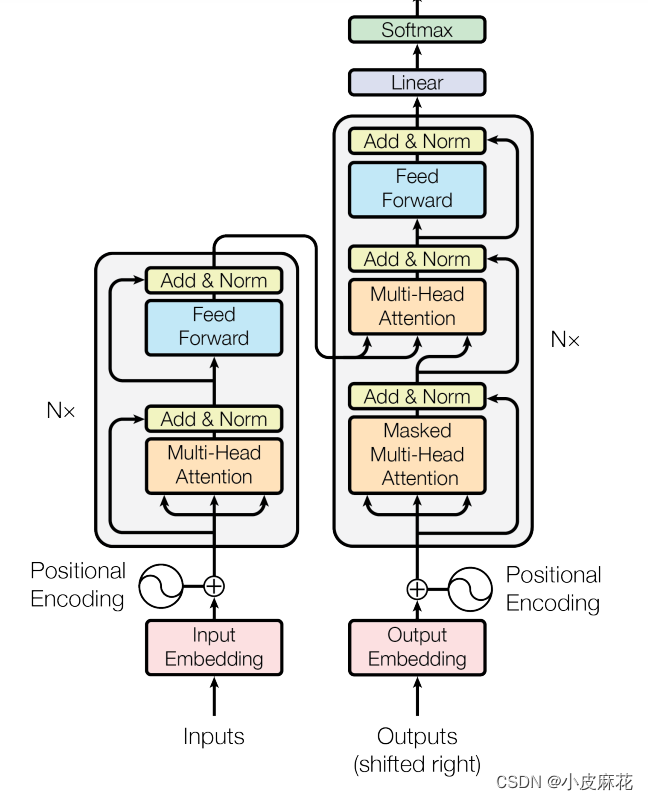
什么是残差连接呢?残差连接就是把网络的输入和输出相加,即网络的输出为F(x)+x,在网络结构比较深的时候,网络梯度反向传播更新参数时,容易造成梯度消失的问题,但是如果每层的输出都加上一个x的时候,就变成了F(x)+x,对x求导结果为1,所以就相当于每一层求导时都加上了一个常数项‘1’,有效解决了梯度消失问题。
Norm操作
首先要明白Norm做了一件什么事,从刚开始接触Transformer开始,我认为所谓的Norm就是BatchNorm,但是有一天我看到了这篇
文章
,才明白了Norm是什么。
假设我们输入的词向量的形状是(2,3,4),2为批次(batch),3为句子长度,4为词向量的维度,生成以下数据:
[[w11, w12, w13, w14], [w21, w22, w23, w24], [w31, w32, w33, w34]
[w41, w42, w43, w44], [w51, w52, w53, w54], [w61, w62, w63, w64]]
如果是在做BatchNorm(BN)的话,其计算过程如下:BN1=(w11+w12+w13+w14+w41+
w42+w43+w44)/8,同理会得到BN2和BN3,最终得到[BN1,BN2,BN3] 3个mean
如果是在做LayerNorm(LN)的话,则会进如下计算:LN1=(w11+w12+w13+w14+w21+
w22+w23+w24+w31+w32+w33+w34)/12,同理会得到LN2,最终得到[LN1,LN2]两个mean
如果是在做InstanceNorm(IN)的话,则会进如下计算:IN1=(w11+w12+w13+w14)/4,同理会得到IN2,IN3,IN4,IN5,IN6,六个mean,[[IN1,IN2,IN3],[IN4,IN5,IN6]]
下图完美的揭示了,这几种Norm
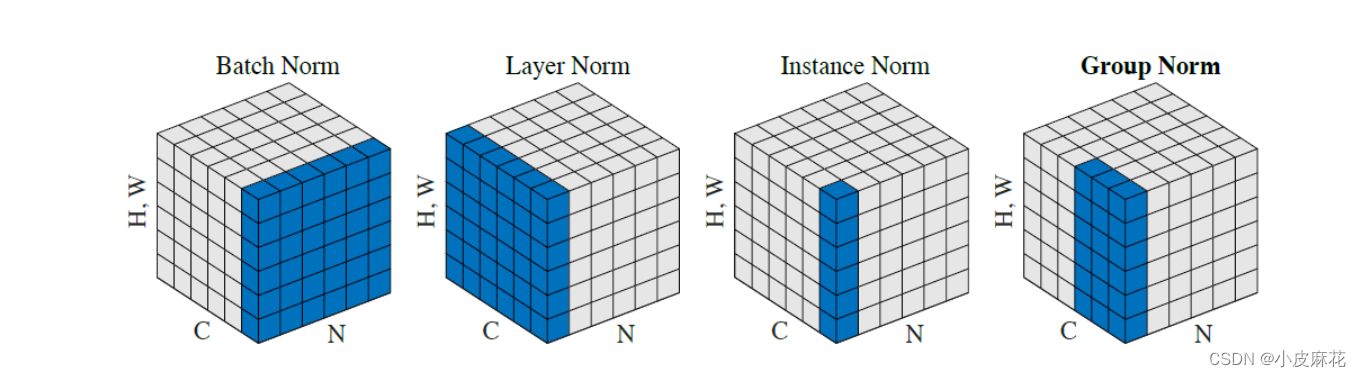
接下来我们来看一下Transformer中的Norm:首先生成[2,3,4]形状的数据,使用原始的编码方式进行编码:
import torch
from torch.nn import InstanceNorm2d
random_seed = 123
torch.manual_seed(random_seed)
batch_size, seq_size, dim = 2, 3, 4
embedding = torch.randn(batch_size, seq_size, dim)
layer_norm = torch.nn.LayerNorm(dim, elementwise_affine = False)
print("y: ", layer_norm(embedding))
输出:
y: tensor([[[ 1.5524, 0.0155, -0.3596, -1.2083],
[ 0.5851, 1.3263, -0.7660, -1.1453],
[ 0.2864, 0.0185, 1.2388, -1.5437]],
[[ 1.1119, -0.3988, 0.7275, -1.4406],
[-0.4144, -1.1914, 0.0548, 1.5510],
[ 0.3914, -0.5591, 1.4105, -1.2428]]])
接下来手动去进行一下编码:
eps: float = 0.00001
mean = torch.mean(embedding[:, :, :], dim=(-1), keepdim=True)
var = torch.square(embedding[:, :, :] - mean).mean(dim=(-1), keepdim=True)
print("mean: ", mean.shape)
print("y_custom: ", (embedding[:, :, :] - mean) / torch.sqrt(var + eps))
mean: torch.Size([2, 3, 1])
y_custom: tensor([[[ 1.1505, 0.5212, -0.1262, -1.5455],
[-0.6586, -0.2132, -0.8173, 1.6890],
[ 0.6000, 1.2080, -0.3813, -1.4267]],
[[-0.0861, 1.0145, -1.5895, 0.6610],
[ 0.8724, 0.9047, -1.5371, -0.2400],
[ 0.1507, 0.5268, 0.9785, -1.6560]]])
可以发现和LayerNorm的结果是一样的,也就是说明Norm是对d_model进行的Norm,会给我们[batch,sqe_length]形状的平均值。
加下来进行batch_norm,
layer_norm = torch.nn.LayerNorm([seq_size,dim], elementwise_affine = False)
eps: float = 0.00001
mean = torch.mean(embedding[:, :, :], dim=(-2,-1), keepdim=True)
var = torch.square(embedding[:, :, :] - mean).mean(dim=(-2,-1), keepdim=True)
print("mean: ", mean.shape)
print("y_custom: ", (embedding[:, :, :] - mean) / torch.sqrt(var + eps))
输出:
mean: torch.Size([2, 1, 1])
y_custom: tensor([[[ 1.1822, 0.4419, -0.3196, -1.9889],
[-0.6677, -0.2537, -0.8151, 1.5143],
[ 0.7174, 1.2147, -0.0852, -0.9403]],
[[-0.0138, 1.5666, -2.1726, 1.0590],
[ 0.6646, 0.6852, -0.8706, -0.0442],
[-0.1163, 0.1389, 0.4454, -1.3423]]])
可以看到BN的计算的mean形状为[2, 1, 1],并且Norm结果也和上面的两个不一样,这就充分说明了Norm是在对最后一个维度求平均。
那么什么又是Instancenorm呢?接下来再来实现一下instancenorm
instance_norm = InstanceNorm2d(3, affine=False)
output = instance_norm(embedding.reshape(2,3,4,1)) #InstanceNorm2D需要(N,C,H,W)的shape作为输入
layer_norm = torch.nn.LayerNorm(4, elementwise_affine = False)
print(layer_norm(embedding))
输出:
tensor([[[ 1.1505, 0.5212, -0.1262, -1.5455],
[-0.6586, -0.2132, -0.8173, 1.6890],
[ 0.6000, 1.2080, -0.3813, -1.4267]],
[[-0.0861, 1.0145, -1.5895, 0.6610],
[ 0.8724, 0.9047, -1.5371, -0.2400],
[ 0.1507, 0.5268, 0.9785, -1.6560]]])
可以看出无论是layernorm还是instancenorm,还是我们手动去求平均计算其Norm,结果都是一样的,由此我们可以得出一个结论:Layernorm实际上是在做Instancenorm!
FeedForward
接下来是FeedForward,FeedForward是Multi-Head Attention的输出做了残差连接和Norm之后得数据,然后FeedForward做了两次线性线性变换,为的是更加深入的提取特征。
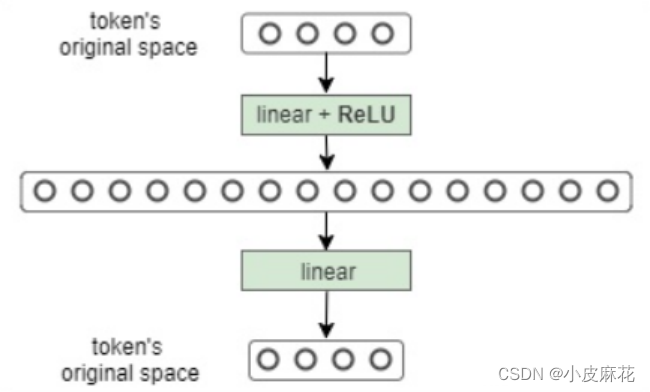
可以看出在每次线性变换都引入了非线性激活函数Relu,在Multi-Head Attention中,主要是进行矩阵乘法,即都是线性变换,而线性变换的学习能力不如非线性变换的学习能力强,FeedForward的计算公式如下:max相当于Relu
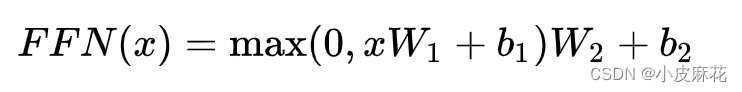
所以FeedForward的作用是:通过线性变换,先将数据映射到高纬度的空间再映射到低纬度的空间,提取了更深层次的特征
MASK
最后是MASK介绍,Transformer中的MASK主要分为两部分:Padding Mask和Sequence Mask两部分
Padding Masked
对于Transformer而言,每次的输入为:[batch_size,seq_length,d_module]结构,由于句子一般是长短不一的,而输入的数据需要是固定的格式,所以要对句子进行处理。
通常会把每个句子按照最大长度进行补齐,所以当句子不够长时,需要进行补0操作,以保证输入数据结构的完整性
但是在计算注意力机制时的Softmax函数时,就会出现问题,Padding数值为0的话,仍然会影响到Softmax的计算结果,即无效数据参加了运算。
为了不让Padding数据产生影响,通常会将Padding数据变为负无穷,这样的话就不会影响Softmax函数了
Self-Attention Masked
Self-Attention Masked只发生在Decoder操作中,在Decoder中,我们的预测是一个一个进行的,即输入一个token,输出下一个token,在网上看到一个很好的解释如下:
假设我们当前在进行机器翻译
输入:我很好
输出:I am fine
接下来是Decoder执行步骤
第一步:
·初始输入: 起始符 + Positional Encoding(位置编码)
·中间输入:(我很好)Encoder Embedding
·最终输出:产生预测“I”
第二步:
·初始输入:起始符 + “I”+ Positonal Encoding
·中间输入:(我很好)Encoder Embedding
·最终输出:产生预测“am”
第三步:
·初始输入:起始符 + “I”+ “am”+ Positonal Encoding
·中间输入:(我很好)Encoder Embedding
·最终输出:产生预测“fine”
上面就是Decoder的执行过程,在预测出“I”之前,我们是不可能知道‘am’的,所以要将数进行Mask,防止看到当前值后面的值,如下图所示:当我们仅知道start的时候,后面的关系是不知道的,所以start和“I”以及其它单词的Score都为负无穷,当预测出“I”之后,再去预测“am”,最终得到下面第三个得分矩阵。
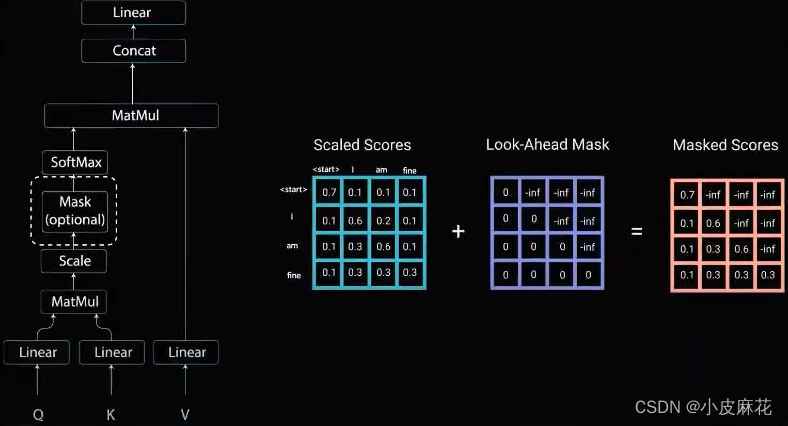
最后经过Softmax处理之后,得到最终的得分矩阵
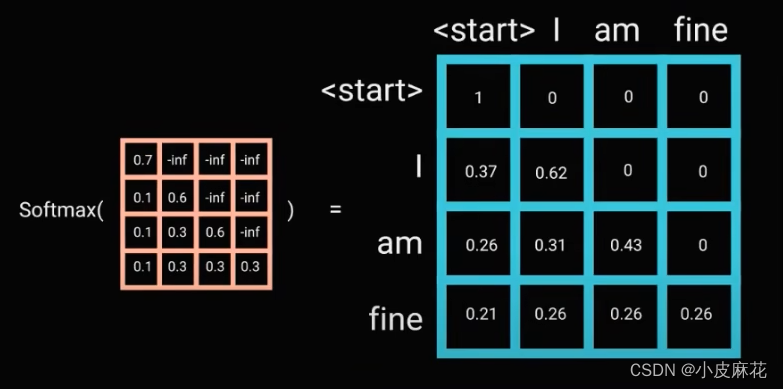
最后不要忘了Decoder中依然采用的是Masked Multi-Head Attention,即多次进行Mask机制
写在最后:笔者也是刚入门深度学习,对知识也是初步的认识,如果文章有错,请大佬们斧正!