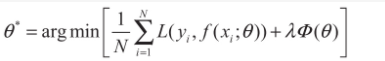二刷,重制
目录
一、图的概述
1.基本概念
1.顶点(Vertex)表示研究的对象,边(Edge)表示两个对象之间特定的研究关系
2.图的存储和遍历
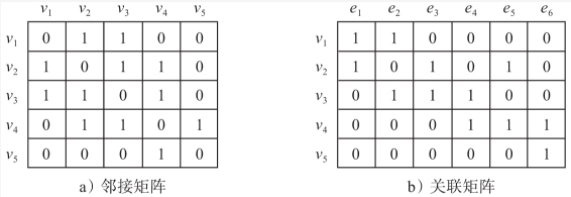
1.存储主要分两种,邻接矩阵(Adjacency matrix)和关联矩阵(Incidence matrix)
邻接矩阵:一维数组表示顶点集合,二维数组表示邻接矩阵A。
用邻接矩阵A描述图中各顶点之间的关联
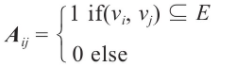
或者用关联矩阵B:用两个一维数组分别表示顶点集和边集,用一个二维数组表示关联矩阵B。
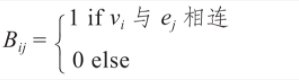
示例图如下

邻接矩阵A和关联矩阵B
2.图的遍历:某点出发,所有顶点访问一次且仅一次
深度(DFS):递归,有回退。一直到头再返回
和广度(BFS,breadth):分层,无回退。先访问第一个所有的邻居,再选择其中一个邻居重复上述
3.应用分类
1.顶点-节点(Node),边-关系(Link)
二、神经网络基础
1.机器学习
1.损失函数(loss function)用来估量模型预测值y*和真实值y的差异程度 通过一次次更新参数Θ 来使损失达到最小
其中,前面的均值函数表示经验风险函数,L表示损失函数,Φ 表示正则化项或者叫惩罚项。
2.梯度下降,利用梯度,通过不断的迭代来更新参数来寻求最优的解(损失最小) 过程:下山时找到最陡的方向(梯度),迈出一步(更新的步长,学习率)。
①通过随机初始化,为要求解的参数赋初值,作为优化的起点。 ②使用模型进行预测,计算总体损失值 ③利用损失值对模型进行求导,得到相应的梯度 ④基于梯度调整参数,得到迭代后的参数
重读上述步骤,直到达到停止的条件若不使用全量样本而使用随机选择的一个样本,用它进行迭代来更新参数,称为随机梯度下降(Stochastic Gradient
Descent,SGD),使用全量样本的称为批梯度下降(Batch Gradient Descent)
2.神经网络
1.激活函数,连续可导,少数点可以不可导。他的非线性可以使神经网络可以任意逼近任何非线性网络,若没有激活函数,每一层输出仍是上一层输入的线形组合,这样的神经网络仍是一个线性模型,表达能力有限
常见的有S型和ReLU型及其变种2.训练神经网络:反向传播(back-propagation),它基于链式法则快速计算参数的梯度,然后使用梯度下降进行参数更新
神经网络运行的过程:前向传播,反向传播,参数更新
①前向传播,给定输入和参数,逐层向前进行计算,最后输出预测结果 ②反向传播:基于前向传播得到的预测结果,使用损失函数得到损失值,然后计算参数的梯度,该计算方法称为反向传播
③参数更新:使用梯度下降算法对参数进行更新,重读上述过程,逐步迭代,直到模型收敛
三、卷积神经网络(CNN)
1.卷积与池化 CNN是具有局部链接、权值共享等特点的深层前馈神经网络。其中两大核心操作就是卷积和池化。
1.卷积 这一词来源于信号处理领域,给定输入信号f和系统响应g,求系统的输出
傅里叶变换是将时域中的数据转换到频域中的一种方法,它将函数分解为一系列不同频率的三角函数的叠加,即找到一道做好的菜具体配料及其用量。
2.池化 主要目的是降维,来降低计算量。常用操作是
平均池化
和
最大化池化
。 池化操作就是使用一个固定大小的滑窗在输入上滑动,每次将滑窗内的元素聚合为一个值作为输出。根据聚合方式,分为平均池化和最大值池化。
2.卷积神经网络
1.卷积神经网络的结构一般分为两个部分: 一部分是由
卷积层和池化层
交替堆叠成的骨干网络,它主要用于从输入中提取丰富的特征; 另一部分是
全连接层
,它将卷积得到的特征图展平,也就是说丢弃了特征图的空间信息,它的主要作用是
聚合全局信息
并映射到输出空间。2.卷积神经网络主要具备以下3个特点:局部连接、权值共享、层次化表达 ①局部连接 卷积计算每次只在卷积核大小对应区域进行,输入和输出是局部连接的。 ②权值共享
不同区域使用卷积核参数,一方面减少了参数量,另一方面带来了平移不变性(无论输入如何平移,总能得到相同的输出) ③层次化表达
卷积网络通过卷积层堆叠得到,每一层都是对前一层进行变换,提取的特征从低层次到高层次,逐渐变得抽象。
四、表示学习
表示即特征,表示学习就是自动从数据中学习“有用”的特征,并可直接用于后续的具体任务
分为①one-hot编码:研究对象➡vector(只在某个维度上是1,其余维度是0)
②分布式表示:例如颜色的RGB三原色编码,用几个来表示多个
五、图信号处理与图卷积神经网络
本章主要是图信号处理的基本理论是如何延伸到图卷积神经网络中的
首先,给出了
图信号
的基本定义,紧接着介绍了
图傅里叶变换
,并由此引出
图信号频率
的定义。然后,介绍图信号上的
滤波操作
,紧接着介绍
卷积滤波
与
图卷积模型
的关系。
### 1.矩阵计算前置知识
矩阵乘法三种方式:A(m
c) B(c
n),C=AB
①内积视角:将A视作一个行向量矩阵,将B视作一个列向量矩阵 C(m*n)=A(m,:)B(:,n) A提供行B提供列(即我们最熟悉得矩阵乘法)
②行向量视角:将B视作一个行向量矩阵,将A视作系数矩阵 C(i,)= ∑A(i m)B(m,:)
③列向量视角:将A视作一个列向量矩阵,将B视作系数矩阵 C(i,)= ∑B(m j)A(:,m)
具体例子见 书P 82
行视角的计算方式对理解空域图卷积的计算逻辑与意义大有帮助
2.图信号与图的拉普拉斯矩阵
1.
图信号
:给定图G=(V,E),图信号是一种描述V➡R的映射,表示成向量的形式:x=[x1,x2,x3,…xn]^T,其中xi是节点vi上信号的强度。
因为图的节点之间有固有的关联结构,所以在研究图信号时,除了考虑信号的强度之外,还要考虑图的拓扑结构
2.
拉普拉斯矩阵(Laplacian Matrix
):是用来研究图的结构性质的核心对象.
关于拉普拉斯矩阵和拉普拉斯算子的介绍看这篇文章
【其实贼简单】拉普拉斯算子和拉普拉斯矩阵

拉普拉斯矩阵的定义来自于拉普拉斯算子,拉普拉斯算子是n维欧氏距离中的一个二阶微分算子,若将算子的作用域退化到离散的二维图像空间,就成了边缘检测算子
拉普拉斯算子描述了中心像素与局部四邻居像素的差异,用于图像上的边缘检测算子。
同理,在图信号中,用来描述中心节点与邻居节点之间的信号的差异
。对于一个函数,拉普拉斯算子实际上衡量了在空间中的每一点处,该函数梯度是倾向于增加还是减少。

3.图傅里叶变换
1.时域和频域:时域和频域是信号的基本性质。
时域(Time domain)
是描述数学函数或物理信号对时间的关系。
频域(Frequency domain)
是描述信号在频率方面特性时用到的一种坐标系。相对于更加直观的时域视角,频域分析则更能体现信号的一些特征和本质。
傅里叶变换
则是将信号从
时域
空间转换到
频域
空间的方法,是数字信号处理的基石。
类比傅里叶变换,书中首先给出图信号傅里叶变换的定义,即将图信号由空域(spatial domain)视角转换成频域视角。在我们得到图信号(这个图信号可以看做是空域视角)的时候,我们就需要进行频域分析(我们需要切换到频域视角来观察图信号的特征),得到图的谱,进而进行谱聚类等操作。
2.拉普拉斯矩阵的一些性质
略
3.图傅里叶变换(Graph Fourier Transform, GFT)
定义:对于任意一个在图G上的信号X,其图傅里叶变换为
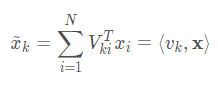
4.图滤波器(Graph Filter)
定义:对给定图信号的频谱中各个频率分量的强度进行增强或衰减的操作。
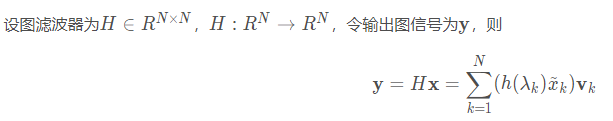


1.空域角度
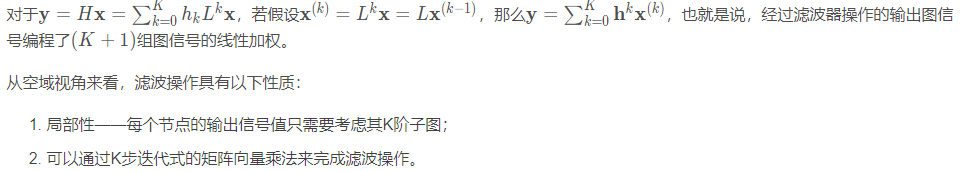
2.频域角度

5.图卷积神经网络(GCN)
先到这,以后再慢慢补