博客

K-Means算法

算法步骤

K-Means算法，即K均值算法，是最常见的一种聚类算法。顾名思义，该算法会将数据集分为K个簇，每个簇使用簇内所有样本的均值来表示，我们将该均值成为‘质心’。具体步骤如下：

1. 从样本中选择K个点作为初始质心
2. 计算每个样本到各个质心的距离，将样本划分到距离最近的质心所对应的簇中。
3. 计算每个簇内所有样本的均值，并使用该均值更新簇的质心。
4. 重复步骤2与3，直到达到以下条件之一结束：
   
   ▷质心的位置变化小于指定的阈值。
   
   ▷达到最大迭代次数。

优化目标

K-Means算法的目标就是选择合适的质心，使得在每个簇内，样本距离质心的距离尽可能的小。这样就可以保证簇内样本具有较高的相似性。我们可以使用最小化簇内误差平方和（within-cluster sum-of-squares SSE）来作为优化算法的量化目标（目标函数），簇内误差平方和也称为簇惯性（inertia）。

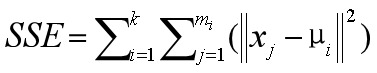
• k：簇的数量。
• m
  
  _i
  
  ：第i个簇含有的样本数量。
• μ
  
  _i
  
  ：第i个簇的质心。
• ||x
  
  _j
  
  – μ
  
  _i
  
  ||：第i个簇中，每个样本x
  
  _j
  
  与质心μ
  
  _i
  
  的距离。

算法优点与缺点

K-Means优点如下：

1. 理解与实现简单。
2. 可以很好的扩展到大量样本中。
3. 广泛应用于不同领域。

同时，K-Means算法也具有一定的缺点：

1. 需要事先指定K值，如果K值选择不当，聚类效果可能不佳。
2. 聚类结果受初始质心的影响，可能会收敛到局部最小值。
3. 适用于凸形的数据分布，对于条形或不规则形状的数据，效果较差。

程序演示

假设班级有50名学生参加期末考试，考试科目为语文、数学，现在想根据分数将学生分成若干个类别。

#首先绘制学生成绩的散点图

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams['font.family'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.size'] = 12

np.random.seed(1) #设置随机种子
#生成样本数据
x = np.random.randint(70,100,size=(50,2)) #从70-100中随机生成100个数，数组形状为50行2列
plt.scatter(x[:, 0], x[:, 1])
plt.xlabel('语文')
plt.ylabel('数学')

#使用sklearn中提供的KMeans类，实现K均值聚类。
#当完成训练后，可以通过KMeans对象获取相关属性值

from sklearn.cluster import KMeans

#n_clusters：簇的数量。
kmeans = KMeans(n_clusters=4)
kmeans.fit(x)
#获取聚类后的质心
print('质心：', kmeans.cluster_centers_)
#获取每个样本所属的簇，标签的数值对应所属簇的索引
print('标签：', kmeans.labels_)
#获取SSE（簇惯性）
print('SSE：', kmeans.inertia_)
#获取迭代次数
print('迭代次数：',kmeans.n_iter_)
#聚类的分值，分值越大，效果越好。直接去SSE的相反数
print('分值:', kmeans.score(x))

我们也可以对训练集之外的样本进行预测，K-Means算法的预测非常简单，就是看待预测样本与哪个质心的距离最近，就将其预测为哪个类别。

unknown = np.array([[76,99],[94,80]])
y_hat = kmeans.predict(unknown)
print(y_hat)

绘制聚类后的效果

#定义绘制聚类结果的函数
def plot_cluster(model, train, test=None):
    color = np.array(['r','g','b','orange'])
    cc = model.cluster_centers_
    label = model.labels_
    plt.scatter(cc[:,0], cc[:,1], marker='+', s=150, c=color)
    plt.scatter(train[:,0], train[:,1], c=color[label])
    if test is not None:
        y_hat = kmeans.predict(test)
        plt.scatter(test[:,0], test[:,1], marker='*', s=150, c=color[y_hat])
        plt.xlabel('语文')
        plt.ylabel('数学')
        plt.title(f'SSE：{model.inertia_:.2f} 迭代次数：{model.n_iter_}')
        
plot_cluster(kmeans, x, unknown)

初始质心的影响

上文提到过，K-Means算法的一个缺点是，容易受到初始质心的影响，即初始质心的不同，可能会导致最后的聚类结果不同。

如下代码为不同初始质心下的聚类结果图。

seed = [10,5]
plt.figure(figsize=(15,5))
for i in range(1,3):
    plt.subplot(1,2,i)
    kmeans = KMeans(n_clusters=4, init='random', n_init=1, random_state=seed[i-1])
    kmeans.fit(x)
    plot_cluster(kmeans,x)

通常情况下，我们会随机初始化多组质心，执行多次，然后选择SSE最小的初始化质心。该操作可以通过n_init参数来指定，该参数默认值为10。

plt.figure(figsize=(15,5))
for i in range(1,3):
    plt.subplot(1,2,i)
    kmeans = KMeans(n_clusters=4, init='random', n_init=10, random_state=seed[i-1])
    kmeans.fit(x)
    plot_cluster(kmeans,x)

可以看到，将n_init参数调整为10后，聚类效果稳定了很多。