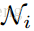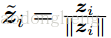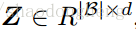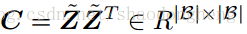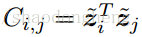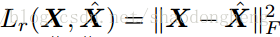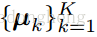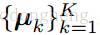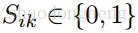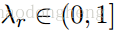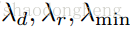Deep Discriminative Latent Space for Clustering 理解梳理

翻译链接：

https://blog.csdn.net/shaodongheng/article/details/83021629

网络结构图：

两个部分的算法：

预训练阶段：

是最大迭代次数，

，

是第 i 次迭代方程：

的结果，

是一个很小的数。

计算数据集原始表示的k最近邻

，

是选择的锚对的集合，

表示该集合的样本数。

锚对：

将k-最近邻图

中具有最大相似性的一部分作为锚对。

设定

作为潜在空间的归一化的表示。

潜在表示矩阵

，其中

表示每一批次的样本数目，将

定义为行归一化批量矩阵（其第i行是行向量

），并且将

定义为成对余弦相似度矩阵，使得

。

α<1是超参数。

最小化损失函数：

其中λ代表正则化强度，即系数，

表示重构损失，X代表原始输入批次的矩阵，

代表Frobenius范数。

由此得到了预训练的自动编码器参数

和自动解码器参数

。

聚类阶段：

第一阶段：

优化过程从

的初始化开始，在整个数据集D上通过优化等式（7），即最大化：

得到初始化的

。

然后我们交替优化参数，即优化一个时其他保持不变，先最大化目标函数得到分配矩阵S，然后最大化得到

，最后最大化得到自动编码器参数。 优化过程迭代直到收敛。

将前面预训练阶段得到的模型参数


，


带入，

是聚类簇的质心，


S


是分配矩阵（权重矩阵）

，

。

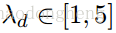
是超参数

初始化

更新

：

更新

和

：

第二阶段：

采用第一阶段得到的参数

初始化。

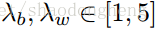
与第一阶段只是优化函数不同：

其中：