数据结构
jdk7内部数据结构为
数组+链表
,通过key的hash值计算数据所在数组下标,多个key的hash相同或hash计算的数组下标相同,但是key值不同时,往链表尾追加Entry。
transient Entry<K,V>[] table = (Entry<K,V>[]) EMPTY_TABLE;static class Entry<K,V> implements Map.Entry<K,V> {
final K key;
V value;
Entry<K,V> next;
int hash;
}
jdk8内部数据结构为
数组+(链表 或 红黑树)
,通过key的hash值计算数据所在数组下标,多个key的hash相同或hash计算的数组下标相同,但是key值不同时,检查节点是否为树节点,是树节点则往树节点添加,如果是普通节点则往链表尾追加Entry,当链表长度大于8时,则将链表转为红黑树。
transient Node<K,V>[] table;static class Node<K,V> implements Map.Entry<K,V> {
final int hash;
final K key;
V value;
Node<K,V> next;
}static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
TreeNode<K,V> parent; // red-black tree links
TreeNode<K,V> left;
TreeNode<K,V> right;
TreeNode<K,V> prev; // needed to unlink next upon deletion
boolean red;
}//LinkedHashMap.Entry
static class Entry<K,V> extends HashMap.Node<K,V> {
Entry<K,V> before, after;
Entry(int hash, K key, V value, Node<K,V> next) {
super(hash, key, value, next);
}
}
HashMap.put源码分析
public V put(K key, V value) {
return putVal(hash(key), key, value, false, true);
}final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
boolean evict) {
Node<K,V>[] tab; Node<K,V> p; int n, i;
if ((tab = table) == null || (n = tab.length) == 0)
//当HashMap的内部table为空时,触发resize()
n = (tab = resize()).length;
if ((p = tab[i = (n - 1) & hash]) == null)
//当通过key的hash值计算数据所在数组下标值为null时直接生成新节点放入桶
tab[i] = newNode(hash, key, value, null);
else {
Node<K,V> e; K k;
if (p.hash == hash &&
((k = p.key) == key || (key != null && key.equals(k))))
//key完全相同
e = p;
else if (p instanceof TreeNode)
//桶内对象已经时红黑树
e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
else {
//桶内已经存在普通节点则遍历链表,往链表尾部添加节点
for (int binCount = 0; ; ++binCount) {
if ((e = p.next) == null) { //第1个循环是获取第2个节点了(0->root.next)
//binCount为0时插入的第二个节点
p.next = newNode(hash, key, value, null);
//如果链表内的数据已经超过8个则将链表转成红黑树
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
//binCount等于7时 即该槽插入第9个节点时(超过8个时)
treeifyBin(tab, hash);
break;
}
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
break;
p = e;
}
}
if (e != null) { // existing mapping for key
V oldValue = e.value;
if (!onlyIfAbsent || oldValue == null)
e.value = value;
afterNodeAccess(e);
return oldValue;
}
}
++modCount;
if (++size > threshold)
resize();
afterNodeInsertion(evict);
return null;
}final void treeifyBin(Node<K,V>[] tab, int hash) {
int n, index; Node<K,V> e;
//检查tab的长度是否大于等于64,小于则扩容
if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
resize();
else if ((e = tab[index = (n - 1) & hash]) != null) {
//将Node对象转为TreeNode 还是默认用双向链表连接
TreeNode<K,V> hd = null, tl = null;
do {
TreeNode<K,V> p = replacementTreeNode(e, null);
if (tl == null)
hd = p;
else {
p.prev = tl;
tl.next = p;
}
tl = p;
} while ((e = e.next) != null);
if ((tab[index] = hd) != null)
//将TreeNode链表转成红黑树
hd.treeify(tab);
}
}final void treeify(Node<K,V>[] tab) {
TreeNode<K,V> root = null;
for (TreeNode<K,V> x = this, next; x != null; x = next) {
next = (TreeNode<K,V>)x.next;
x.left = x.right = null;
if (root == null) {
//root为空时直接第一个元素存入root
x.parent = null;
x.red = false;
root = x;
}
else {
K k = x.key;
int h = x.hash;
Class<?> kc = null;
//往二叉树中插入当前节点
for (TreeNode<K,V> p = root;;) {
int dir, ph;
K pk = p.key;
if ((ph = p.hash) > h)//优先直接比较hash值
dir = -1;
else if (ph < h)//优先直接比较hash值
dir = 1;
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) || //hash值相同则判断key是否实现Comparable接口
(dir = compareComparables(kc, k, pk)) == 0) //实现了Comparable接口则直接比较
//没有实现Comparable接口则用System.identityHashCode比较
dir = tieBreakOrder(k, pk);
TreeNode<K,V> xp = p;
//检查树节点是否为空,不为空继续比较,直到找到空的节点放入当前节点。
if ((p = (dir <= 0) ? p.left : p.right) == null) {
x.parent = xp;
if (dir <= 0)
xp.left = x;
else
xp.right = x;
//进行二叉树平衡操作
root = balanceInsertion(root, x);
break;
}
}
}
}
//将root接口放入table的第一个元素
moveRootToFront(tab, root);
}static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,
TreeNode<K,V> x) {
//新增节点默认红色
x.red = true;
//xp 父节点
//xpp 爷爷节点
//xppl 左叔父节点
//xppr 右叔父节点
for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
//判父节点
if ((xp = x.parent) == null) {
//父节点为null,即root,直接将颜色设置为黑色,返回
x.red = false;
return x;
}
else if (!xp.red || (xpp = xp.parent) == null)
//父节点为黑色节点 或 爷爷节点不存在(即父节点为root节点)
return root;
if (xp == (xppl = xpp.left)) {
//父节点是爷爷的左子节点
if ((xppr = xpp.right) != null && xppr.red) {
//右叔父节点存在且为红色 则颜色反转变黑色
//图解
// xppr
// xppl xppr(red)
// x
//右叔父节点 变黑色
xppr.red = false;
//父节点(即左叔父)节点为黑色
xp.red = false;
//爷爷节点红色
xpp.red = true;//因为黑节点的父亲必须红色
//向上跨越到爷爷节点 继续
x = xpp;
}
else {
//右叔父节点不存在 或存在但为黑色
if (x == xp.right) {
//当前节点为父亲节点的右子节点
//图解
//第一种情况
// xppr(red)
// xppl(black) xppr(black)
// x
//第二种情况
// xppr
// xppl
// x
// 向上跨越到父亲节点
// 再进行左旋
root = rotateLeft(root, x = xp);
// 爷爷节点不存在则over 存在则向上跨越一代
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null) {
//父节点不为空
//变黑色
xp.red = false;
if (xpp != null) {
//爷爷节点存在 变红色 因为黑节点的父亲必须红色
xpp.red = true;
//右旋
root = rotateRight(root, xpp);
}
}
}
}
else {
//当前节点的父节点是右子节点
if (xppl != null && xppl.red) {
//即当前节点的父节点以及父节点的兄弟节点(即左叔父)都是红色 则颜色反转变黑色
xppl.red = false;
xp.red = false;
xpp.red = true; //因为黑节点的父亲必须红色
//向上跨越到爷爷节点 继续
x = xpp;
}
else {
//左叔父节点不存在 或存在但为黑色
if (x == xp.left) {
//当前节点是父亲节点的左儿子
// 向上跨越到父亲节点
// 再进行右旋
root = rotateRight(root, x = xp);
// 爷爷节点不存在则over 存在则向上跨越一代
xpp = (xp = x.parent) == null ? null : xp.parent;
}
//注意已经上跨一代
if (xp != null) {
//父节点不为空
//则变色
xp.red = false;
if (xpp != null) {
//爷爷节点存在 变红色 因为黑节点的父亲必须红色
xpp.red = true;
//左旋
root = rotateLeft(root, xpp);
}
}
}
}
}
}后边就是大家熟知的左右旋转了
/* ------------------------------------------------------------ */
// Red-black tree methods, all adapted from CLR
static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,
TreeNode<K,V> p) {
TreeNode<K,V> r, pp, rl;//r右子节点 pp父节点 p父节点 pp爷爷节点
if (p != null && (r = p.right) != null) {
//r 右节点存在
if ((rl = p.right = r.left) != null)
rl.parent = p;
if ((pp = r.parent = p.parent) == null)
(root = r).red = false;
else if (pp.left == p)
pp.left = r;
else
pp.right = r;
r.left = p;
p.parent = r;
}
return root;
}
static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root,
TreeNode<K,V> p) {
TreeNode<K,V> l, pp, lr;
if (p != null && (l = p.left) != null) {
if ((lr = p.left = l.right) != null)
lr.parent = p;
if ((pp = l.parent = p.parent) == null)
(root = l).red = false;
else if (pp.right == p)
pp.right = l;
else
pp.left = l;
l.right = p;
p.parent = l;
}
return root;
}
链表转红黑树过程示意图:
借哈别人的图

总结:
平衡二叉树
1)简介
AVL树是带有平衡条件的二叉查找树,一般是用平衡因子差值判断是否平衡并通过旋转来实现平衡,
左右子树树高不超过1
,和红黑树相比,AVL树是严格的平衡二叉树,平衡条件必须满足(
所有节点的左右子树高度差不超过1
)。不管我们是执行插入还是删除操作,只要不满足上面的条件,就要通过旋转来保持平衡,而的
旋转非常耗时
的,由此我们可以知道
AVL树适合用于插入与删除次数比较少,但查找多的情况
(2)局限性
由于
维护这种高度平衡所付出的代价比从中获得的效率收益还大
,故而实际的应用不多,更多的地方是用追求局部而不是非常严格整体平衡的红黑树。当然,如果应用场景中
对插入删除不频繁,只是对查找要求较高,那么AVL还是较优于红黑树
。
(3)应用
1,Windows NT内核中广泛存在;
红黑树
(1)简介
一种二叉查找树,但在
每个节点增加一个存储位表示节点的颜色
,可以是
红或黑
(非红即黑)。通过对任何一条从根到叶子的路径上各个节点着色的方式的限制,
红黑树确保没有一条路径会比其它路径长出两倍
,因此,红黑树是一种
弱平衡二叉树
(由于是弱平衡,可以看到,在相同的节点情况下,AVL树的高度低于红黑树),
相对
于要求严格的
AVL树来说
,它的
旋转次数少
,所以对于
搜索,插入,删除操作较多的情况下,红黑树效率更高
。
(2)性质
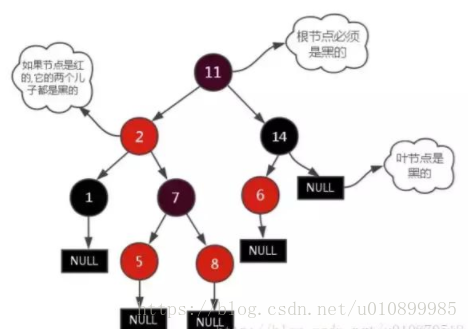
如图1所示,每个节点非红即黑;
1.
每个节点非红即黑
2.
根节点是黑的
;
3.
每个叶节点(此叶节点是树尾端NULL指针或NULL节点,不是我们平时说的非null的叶子节点哦)都是黑的
;
4. 如图所示,如果
一个节点是红的,
那么
它的两儿子都是黑的(黑节点的父亲必红)
;
5.
对于任意节点而言,其到叶子点树(NULL指针叶子)到root节点,每条路径都包含相同数目的黑节点
;
6. 每条路径都包含相同的黑节点;
(3)应用
1,广泛用于C ++的STL中,地图和集都是用红黑树实现的;
2,着名的Linux的的进程调度完全公平调度程序,用红黑树管理进程控制块,进程的虚拟内存区域都存储在一颗红黑树上,每个虚拟地址区域都对应红黑树的一个节点,左指针指向相邻的地址虚拟存储区域,右指针指向相邻的高地址虚拟地址空间;
3,IO多路复用的epoll的的的实现采用红黑树组织管理的的的sockfd,以支持快速的增删改查;
4,Nginx的的的中用红黑树管理定时器,因为红黑树是有序的,可以很快的找到距离当前最小的定时器;
5,Java的的的中TreeMap 、HashMap(1.8以后版本)中的实现;