简单选择排序（顺序存储、链式存储）、堆排序（顺序存储）

选择排序分为简单选择排序和堆排序。其基本思想是：每一趟（如第i趟）在后面n-i+1（i=1,2，…，n-1）个待排序元素中选关键字最小的元素，作为有序子序列的第i个元素，直到第n-1趟做完，待排序元素只剩下1个，就不用再选了。

简单选择排序

算法思想：假设排序表为L[1…n]，第i趟排序即从L[i…n]中选取关键字最小的元素与L(i)交换，每一趟排序可以确定一个元素的最终位置，这样经过n-1趟排序就可以使得整个排序表有序。


顺序存储结构（数组）

/*
Title:简单选择排序（数组结构实现）
Author:F&S&L 
Time:2020.11.30 
*/
#include<stdio.h>
#include<stdlib.h>
#define MaxSize 100

int A[MaxSize];        //初始化数组 

int CreateA()         //创建待排序数组A[] 
{
	int e,i=0;
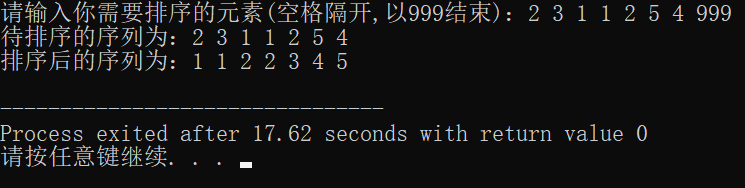
	printf("请输入你需要排序的元素(空格隔开,以999结束)：");
	while(1)
	{
		scanf("%d",&e);
		if(e!=999)    //当从键盘输入的元素不为999时，就存储到数组A[]中；反之，则结束输入 
		{
			i++;      //i记录的是待排序数组中元素的个数 
			A[i-1]=e;
		} 
		else break;
	}
	return i-1;	    //返回的i-1表示的是待排序数组中最后一个元素的下标 
} 

void SelectSort(int rear)  //简单选择排序函数，传入的参数rear表示的是最后一个元素的小标 
{
	int front=0,p,temp;   //front是进行比较的第一个元素的位置，p是用来记录当前比较过程中最小元素的位置，temp是交换元素的盒子 
	while(front<rear)  //结束循环的条件 
	{
		p=front;       //假设当前最小元素的front 
		for(int i=front+1;i<=rear;i++)   //如果i位置的元素小于p位置元素的值，则将i赋给p 
		{
			if(A[i]<A[p])
			{
				p=i;
			}
		}
		temp=A[front];    //一趟之后，就进行元素交换，把最小元素赋给front位置，同时front+1，再进行下一趟 
		A[front]=A[p];
		A[p]=temp;
		front++;
	}
}

void PrintfA(int rear)   //打印数组A[] 
{
	for(int i=0;i<=rear;i++)
	{
		printf("%d ",A[i]);	
	}
	printf("\n");	
} 

int main()
{
	int n;
	n=CreateA();
	printf("待排序的序列为：");
	PrintfA(n); 
	SelectSort(n);
	printf("排序后的序列为：");
	PrintfA(n); 
}

链式存储结构（单链表）

/*
Title:简单选择排序（单链表结构实现）
Author:F&S&L 
Time:2020.11.30 
*/
#include<stdio.h>
#include<stdlib.h>
#define ElemType int

typedef struct Lnode  //创建节点的数据结构 
{
	ElemType data;
	struct Lnode *next;
}LNode,*LinkList;

LinkList CreateList()  //尾插法创建单链表 
{
	ElemType e=0;
	LinkList L;
	L=(LinkList)malloc(sizeof(Lnode));
	LNode *s,*r=L;          //节点s用来存储待插入元素，指针r用来指向当前链表的尾部 
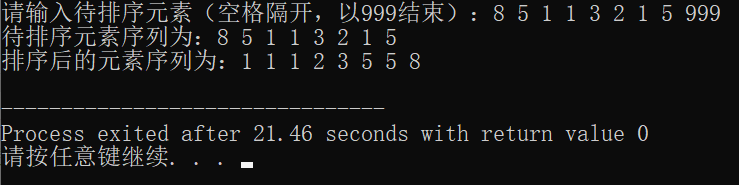
	printf("请输入待排序元素（空格隔开，以999结束）：");
	while(e!=999)
	{
		scanf("%d",&e);
		if(e!=999)
		{
			s=(LNode*)malloc(sizeof(Lnode));
			s->data=e;
			r->next=s;
			r=s;
		}
		else
		{
			r->next=NULL;
			break;
		}
	}
	return L;
}

LinkList SelectSort(LinkList L)
{
	LNode *front=L->next;   //front指针指向待排序序列的第一个元素 
	LNode *p;       //指针p用来指向来比较的元素 
	LNode *min;     //指针min用来指向当前最小元素的位置 
	int temp;		//temp作为交换元素的空间 
	while(front->next!=NULL)   //当front没有指向最后一个元素时 
	{
		min=front;
		p=front->next;
		while(p->next!=NULL)
		{
			if(p->data<min->data)
			{
				min=p;
				p=p->next;
			}
			else 
			{
				p=p->next;
			}
		}
		if(p->data<min->data)min=p;   //当front指向最后一个元素时，比较最后一个元素和当前min的大小 
		temp=front->data;        //将一趟下来min指向的值和front指向的值交换 
		front->data=min->data;
		min->data=temp;
		front=front->next;     //再将front指针后移一个位置 
	}
	return L;
} 

void PrintfList(LinkList L)
{
	LNode *p=L->next;
	while(p->next!=NULL)
	{
		printf("%d ",p->data);
		p=p->next;
	}
	printf("%d",p->data);
	printf("\n");
}

int main()
{
	LinkList L;
	L=CreateList();
	printf("待排序元素序列为：");
	PrintfList(L);
	SelectSort(L);
	printf("排序后的元素序列为：");
	PrintfList(SelectSort(L)); 
}

空间效率：O（1）

时间效率：O（n^2）

稳定性：不稳定

堆排序

算法思想：首先将存放在L[1…n]中的n个元素建成初始堆，由于堆（大根堆）本身的特点，堆顶元素就是最大值。输出堆顶元素之后，通常将堆底元素送到堆顶，此时根节点已经不满足大根堆性质，堆被破坏，将堆顶元素向下调整使其继续保持大根堆的性质，再输出堆顶元素。如此重复，直到堆中只有一个元素为止。


数组实现，基于树的顺序存储特点，i节点的左孩子是2i，右孩子是2i+1

/*
Title:堆排序（数组实现，基于树的顺序存储特点，i节点的左孩子是2i，右孩子是2i+1）
Author:F&S&L 
Time:2020.12.1 
*/
#include<stdio.h>
#include<stdlib.h>
#define MaxSize 100

int A[MaxSize];

//用户输入待排序元素序列
int CreateA()
{
    int e,len=0;
    printf("请输入待排序元素序列（空格隔开，以999结束）：");
    while(1)
    {
        scanf("%d",&e);
        if(e!=999)
        {
            len++;
            A[len]=e;
        }
        else
        {
            break;
        }
        
    }
    return len;   //返回待排序元素序列的长度，即元素个数
}

//建立大根堆
void BuildMaxHeap(int A[],int len)   //预留0号位置来作为交换元素的空间
{
    int i=len/2;
    while(i>0)
    {
        if(2*i+1<=len)     //当i号位置的右孩子存在时
        {
            if(A[2*i]>A[i]&&A[2*i+1]>A[i])  //如果左孩子和右孩子同时大于父亲节点
            {
                if(A[2*i]-A[2*i+1]>=0)    //得比较左右孩子的值，较大的那个和父亲节点交换元素
                {
                    A[0]=A[2*i];
                    A[2*i]=A[i];
                    A[i]=A[0];
                }
                else
                {
                    A[0]=A[2*i+1];
                    A[2*i+1]=A[i];
                    A[i]=A[0];
                }                
            }
            if(A[2*i]>A[i])   //右孩子小于父亲节点，左孩子大于父亲节点
            {
                A[0]=A[2*i];
                A[2*i]=A[i];
                A[i]=A[0];
            }
            if(A[2*i+1]>A[i])   //左孩子小于父亲节点，右孩子大于父亲节点
            {
                A[0]=A[2*i+1];
                A[2*i+1]=A[i];
                A[i]=A[0];
            }
        }
        i--;     //交换元素后，使i的值减1
    }
}

//进行堆排序
void HeapSort(int A[],int len)
{
    BuildMaxHeap(A,len);
    for(int i=len;i>1;i--)     //交换根和当前最后一个元素的值
    {
        A[0]=A[i];
        A[i]=A[1];
        A[1]=A[0];
        BuildMaxHeap(A,i-1);   //交换结束后，最大的元素就在最后（就可以忽视它），再使当前数组长度减1，进行堆排序，使最大的元素跑到根节点位置
    }
}

//打印数组A中的元素
void PrintfA(int A[],int len)
{
    for(int i=1;i<=len;i++)
    {
        printf("%d ",A[i]);
    }
    printf("\n");
}

int main()
{
    int len=CreateA();
    printf("待排序元素序列为：");
    PrintfA(A,len);
    HeapSort(A,len);
    printf("排序后的元素序列为：");
    PrintfA(A,len);
}

空间效率：O（1）

时间效率：O（nlog2n）

稳定性：不稳定