论文汇总
链接:
http://pan.baidu.com/s/1i3waHBR
密码: cfy5
个人感觉讲的比较清楚的(百度云里都包括,贴一下百度文库方便查看)
The Magical Splay
BST 拓展与伸展树 (Splay) 一日通
杨思雨 2004国家集训队论文 《伸展树的基本操作与应用》
浅谈平衡树
平衡树种类
-
平衡树通过旋转操作来使自身达到平衡状态,这其中例如Treap,Splay是均摊
O
(
l
o
g
N
)
,而例如SBT是严格平衡严格
O
(
l
o
g
N
)
平衡树性质
- 对于一个节点i,它的leftson[i] (包括一个点或整个子树)的权值都小于节点i,它的rightson[i] (包括一个点或整个子树)的权值都大于节点i
- 平衡树是依靠整棵树的中序遍历来维护整个序列的
Splay的旋转和伸展操作
旋转
Splay分为左旋(zag),右旋(zig),通过组合我们又可以得到zig-zig,zag-zag,zig-zag,其中可以证明zig-zag=zig+zag,所以我们只需要zig,zag,zig-zig,zag-zag,考虑对称性,就分为单旋和双旋了
单旋
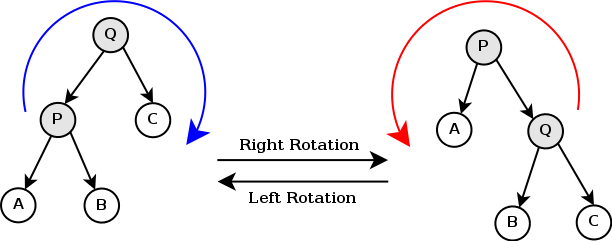
双旋
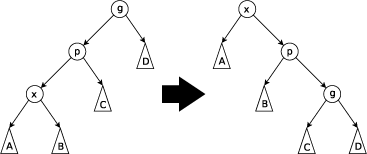
- 对于双旋我们也是可以把它摘成两步单旋的
- 比如上图,我们先对p右旋,再对x右旋即可
- 综上就只有左右单旋就可实现所有旋转操作了
- 从code角度来讲,左右旋是可以写成一个的
- w[a,i],i=1:左儿子2:右儿子3:父4:子树节点和5:该权值个数6:权值
-
特意说一下w[a,5]:该权值个数,他存在的原因是因为插入时可能是重复的,而旋转操作的其中一个原因是二叉树的
严格
左儿子<该节点<右儿子,所以插入时重复的直接在w[a,5]上+1即可
procedure rotate(a,kind:longint); //kind=1右旋;kind=2左旋
var b,unkind;
begin
b:=w[a,3]; unkind:=kind xor 3;
w[a,4]:=w[b,4]; dec(w[b,4],w[a,5]+w[w[a,kind],4]);
w[w[a,unkind],3]:=b; w[b,kind]:=w[a,unkind];
w[a,unkind]:=b; w[a,3]:=w[b,3]; w[b,3]:=a;
if w[a,3]<>-1
then
if w[w[a,3],1]=b
then w[w[a,3],1]:=a
else w[w[a,3],2]:=a;
end;
伸展
Splay的均摊复杂度为每次O(logN)就是靠着每次将要操作的节点提为根节点来维持的
以下我们以a为操作节点,b=fa[a]来说
我
们
定
义
a
为
它
父
节
点
的
左
儿
子
(
s
o
n
[
b
,
1
]
=
a
)
那
么
k
i
n
d
=