卡方检验(chi square test)能够是一种假设性检验的方法,它能够检验两个分类变量之间是否是独立无关的。它通过观察实际值和理论值的偏差来确定原假设是否成立,它按照以下步骤来检验两个分类变量是否是独立的。
无关性假设
假如,有了一些新闻文章,这些新闻的文章已经标好了类别,所以可以得到以下统计的信息。通过下面的表格的第一行和第二行可以得出,
文章的内容是否包含“篮球”
的确对
文章是否是体育类别
的有统计上的差别。但是这个值要相差多大才能说明问题呢?这就要用到卡方检验了。
| 组别 | 体育 | 非体育 | 合计 |
| 包含“篮球” | 34 | 10 | 44 |
| 不包含“篮球” | 19 | 24 | 43 |
| 合计 | 53 | 34 | 87 |
用抽样的概率近似与整体的概率,可以得到随机的一个新闻文章,其属于体育类别的概率是:(34 + 19)/ (34 + 19 + 10 + 24) = 0.609。
无关性假设是:
文章是否包含“篮球“
与
文章是否属于体育类别
是独立无关的。那么根据上面得到的概率,可以得到下面的表格。
理论值四格表
如果
文章是否包含“篮球“
与
文章是否属于体育类别
是独立无关的。且一个新闻文章属于体育类别的概率是0.609,那么可以得到下面的表格。因为
文章是否包含“篮球“
与
文章是否属于体育类别
是独立无关的,所以不管文章中是不是包含”篮球“,其属于体育类别的概率都是0.609。
如果两个分类变量真的是独立无关的,那么四格表的实际值与理论值得差值应该非常小(有差值的原因是因为抽样误差)。那么如何衡量实际值与理论值得差值呢?
| 组别 | 体育 | 非体育 |
| 包含”篮球“ | 44 * 0.609 = 26.8 | 44 * 0.391 = 17.2 |
| 不包含”篮球“ | 43 * 0.609 = 26.2 | 43 * 0.391 = 16.8 |
卡方检验公式
卡方检验的公式如下,其中A为实际值,也就是第一个四格表中的四个数据。T为理论值,也就是理论四格表中的四格数据。
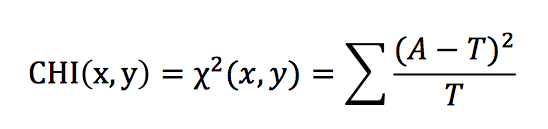
X2值用于衡量实际值与理论值得差异程度,包含了以下两个信息:
- 实际值与理论值偏差的绝对大小(由于平方的存在,差异被放大了)
- 差异值与理论值得相对大小。
上述场景的CHI = 10.10
上面的公式还可以进一步进行化简为下面的公式:
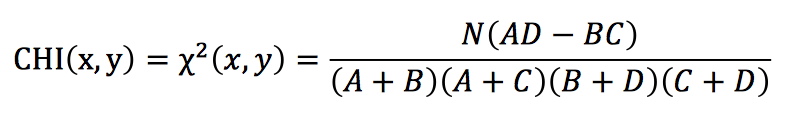
| 组别 | 体育 | 非体育 | 合计 |
| 包含“篮球” | 34 (A) | 10(B) | 44(A+B) |
| 不包含“篮球” | 19(C) | 24(D) | 43(C+D) |
| 合计 | 53(A+C) | 34(B+D) | 87(N) |
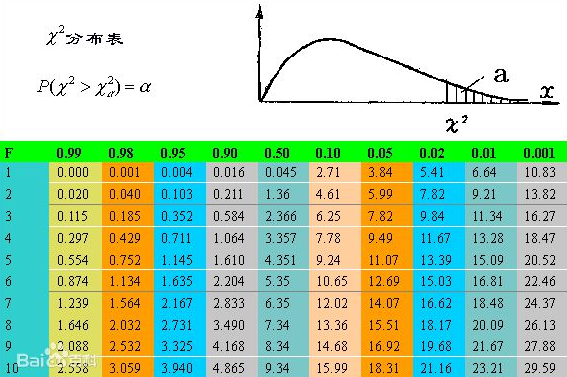
卡方分布的临界值
当通过上述的公式计算得到CHI的值以后,该如何判断我们的原假设是否成立呢?可以通过查询卡方分布的临界值表来查看我们的原假设是否成立。
自由度F = (行数 – 1) * (列数 – 1) = 1,对于四格表,F = 1。
由于自由度F = 1,所以只需要看分布表的第一行。可以看到,随着CHI的增大,原假设成立的概率就越小。因为10.10 > 6.64,所以原假设成立是概率是小于1%。反之,也就是说,原假设不成立(即两个分类变量不是独立无关)的概率大于99%。
如何应用于特征选择
CHI值越大,说明两个变量越不可能是独立无关的,也就是说X2越大,两个变量的相关程序也就越高。对于特征变量x1,x2,…,xn,以及分类变量y。只需要计算CHI(x1, y)、CHI(x2, y)、…、CHI(xn, y),并按照CHI的值从大到小将特征排序,然后选择阈值,大于阈值的特征留下,小于阈值的特征删除。这样就筛选出一组特征子集了,接着使用这组特征子集去训练分类器,然后评估分类器的性能。
因为只要比较CHI值得相对大小,所以上述的分布表就没用了。
参考:
卡方检验基础:
http://blog.csdn.net/idatamining/article/details/8564966
卡方检验原理及应用:
https://segmentfault.com/a/1190000003719712
卡方检验用于特征选择:
http://blog.csdn.net/idatamining/article/details/8564981
转载于:https://my.oschina.net/u/1779843/blog/889694