js浮点数四则运算精度丢失以及tofixed精度丢失解决方法
一、js浮点数计算精度丢失的一些例子
1、四则运算精度丢失:
0.1+0.2 = 0.30000000000000004
0.3 - 0.2 = 0.09999999999999998
10.22*100 = 1022.0000000000001
2.4/0.8 = 2.9999999999999996
32.2*100 = 3220.0000000000005
32.2*1000 = 32200.000000000004
(32.2*100 + 3.14*100) / 100 = 35.34 // 这里的精度怎么又不丢失了?
32.3*100 = 3229.9999999999995
32.3*1000 = 32299.999999999996
...
2、toFixed() 四舍五入精度丢失:
(1.335).toFixed(2); // '1.33'
(6.265).toFixed(2); // '6.26'
二、浮点数计算精度丢失的原因
js采用64位浮点数表示法(几乎所有现代编程语言所采用),这是一种二进制表示法。二进制浮点数表示法并不能精确表示类似 0.1 这样简单的数字。
这个问题不只在js中才会出现,在任何使用二进制浮点数的编程语言中都会出现。
JavaScript的未来版本或许会支持十进制数字类型以避免精度丢失的问题。
三、解决办法
1、使用 big.js(如果有大量连续的计算推荐使用)
- 既解决了浮点数计算精度丢失问题,又解决了 toFixed() 四舍五入精度丢失问题。
big.js
是
big.js
,
bignumber.js
,
decimal.js
三姐妹中功能最少的,但也是体积最小的,压缩版只有
3k
,对于处理js精度丢失已经足够用了。
import Big from 'big.js'
// 运算
const plus = Big(0.1).plus(0.2); // 加
const minus = Big(0.3).minus(0.1); // 减
const mul = Big(10.22).times(100); // 乘
const div = Big(2.4).div(0.8); // 除
// toFixed
const fixed = new Big(6.265).toFixed(2); // 6.27
console.log(
plus.toNumber(),
minus.toNumber(),
mul.toNumber(),
div.toNumber()
)
// 0.3 0.2 1022 3
2、解决四则运算精度丢失问题
方法1:没有具体要求保留几位小数的,最简单的方法是直接用
toFixed()
toFixed()
从上面四则运算精度丢失的例子可以看到,四则运算的精度丢失主要会出现很多位 0 或很多位 9。
function precision(val) {
return +val.toFixed(8);
}
precision(0.1 + 0.2)
方法2:有具体要求精确到第几位,用
科学计数法
对运算结果进行四舍五入
科学计数法
MDN
已经给出了具体代码(也是利用“科学计数法”扩大 10 的 n 次不会出现精度丢失的特性):
function round(number, precision) {
return Math.round(+number + 'e' + precision) / Math.pow(10, precision);
}
round(1.005, 2); //1.01
round(1.002, 2); //1
或者:
/**
* Decimal adjustment of a number.
*
* @param {String} type The type of adjustment.
* @param {Number} value The number.
* @param {Integer} exp The exponent (the 10 logarithm of the adjustment base).
* @returns {Number} The adjusted value.
*/
function decimalAdjust(type, value, exp) {
// If the exp is undefined or zero...
if (typeof exp === 'undefined' || +exp === 0) {
return Math[type](value);
}
value = +value;
exp = +exp;
// If the value is not a number or the exp is not an integer...
if (isNaN(value) || !(typeof exp === 'number' && exp % 1 === 0)) {
return NaN;
}
// Shift
value = value.toString().split('e');
value = Math[type](+(value[0] + 'e' + (value[1] ? +value[1] - exp : -exp)));
// Shift back
value = value.toString().split('e');
value = +(value[0] + 'e' + (value[1] ? +value[1] + exp : exp));
return value;
}
export default {
round: (value, exp) => {
return decimalAdjust('round', value, exp);
},
floor: (value, exp) => {
return decimalAdjust('floor', value, exp);
},
ceil: (value, exp) => {
return decimalAdjust('ceil', value, exp);
}
};
实现原理:
比如 1022.0000000000001 要保留2位小数,先用 e2 把这个数扩大 100 倍,
再用 Math.round(), Math.floor(), Math.ceil() 取整,然后再用 e-2 缩小回来。
使用方法:
Decimal.round(val, precision)
console.log(Decimal.round(1.13265, -3)) //1.133
console.log(Decimal.round(3.17, -3)) //3.17
console.log(Decimal.round(0.1+0.2, -3)) //0.3
console.log(Decimal.round(3.17)) //3
console.log(Decimal.round(3.17, 0)) //3
console.log(Decimal.round(31216, 1)) //31220
console.log(Decimal.round(31213, 2)) //31200
precision 可选值:不传,0,负数,正数。
- 不传、0: 精确到整数。
- 正数: 1就是个位为0,十位是个位四舍五入的值。
- 负数: 精确到小数点后几位
3、解决 toFixed() 精度丢失问题:重写 toFixed 方法(重点!!!!)
function toFixed(number, precision = 2) {
number = Math.round(+number + 'e' + precision) / Math.pow(10, precision) + '';
let s = number.split('.');
if ((s[1] || '').length < precision) {
s[1] = s[1] || '';
s[1] += new Array(precision - s[1].length).fill('0').join('');
}
return s.join('.');
}
toFixed(6) // '6.00'
四、判断小数是否相等
function epsEqu(x,y) {
return Math.abs(x - y) < Math.pow(2, -52);
// 因为 Number.EPSILON === Math.pow(2, -52),所以也可以这么写:
// return Math.abs(x - y) < Number.EPSILON;
}
// 举例
0.1 + 0.2 === 0.3 // false
epsEqu(0.1 + 0.2, 0.3) // true
小数比较时,要给它一个误差范围,在误差范围内的都算相等。
五、其他由浮点数引起的问题
parseInt(0.0000008) // -> 8
六、项目内实际应用
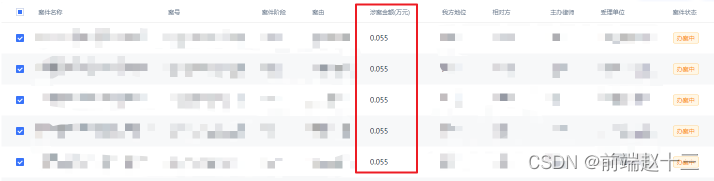
在列表上勾选5个涉案金额为
0.055
万元的案件,进行批量结案操作,在批量结案中,有一个减损值的计算,通过计算
勾选案件涉案金额平均值-用户所填写的结案支付金额得出减损值
,那么问题出现了,我在结案支付金额填写为
0.055
,正常计算的话结果应改为
0
,可是截图却如图所示:

这里的业务代码为:
// 批量结案涉案金额取勾选数据的平均值
const amountInvolved = selectedRows.reduce((c, R) => c + (R.amountInvolved - 0), 0) / selectedRows.length
//计算减损值
OnchangeMoney(value) {
this.mdl.impairmentValue = this.req.amountInvolved - value
},
打断点发现是计算平均值
amountInvolved
时出现了
浮点数
,那么封装一个方法:
function strip(num, precision = 12) {
return +parseFloat(num.toPrecision(precision));
}
为什么选择 12 做为默认精度?
这是一个经验的选择,一般选12就能解决掉大部分0001和0009问题,
而且大部分情况下也够用了,如果你需要更精确可以调高。
- 处理平均数计算:
// 批量结案涉案金额取勾选数据的平均值
const amountInvolved = this.strip(
selectedRows.reduce((c, R) => c + (R.amountInvolved - 0), 0) / selectedRows.length
)
- 运行之后发现还是有浮点数,打断点是计算差值是也出现了浮点数,解决:
//计算金额
OnchangeMoney(value) {
this.mdl.impairmentValue = this.strip(this.req.amountInvolved - value)
},
参考(JS 计算最小值,最大值,平均值,标准差,中位数):
// @numbers 包含所有数字的一维数组
// @digit 保留数值精度小数位数,默认两位小数
function getBebeQ(numbers, digit = 2) {
// 修复js浮点数精度误差问题
const formulaCalc = function formulaCalc(formula, digit) {
let pow = Math.pow(10, digit);
return parseInt(formula * pow, 10) / pow;
};
let len = numbers.length;
let sum = (a, b) => formulaCalc(a + b, digit);
let max = Math.max.apply(null, numbers);
let min = Math.min.apply(null, numbers);
// 平均值
let avg = numbers.reduce(sum) / len;
// 计算中位数
// 将数值从大到小顺序排列好,赋值给新数组用于计算中位数
let sequence = [].concat(numbers).sort((a,b) => b-a);
let mid = len & 1 === 0 ?
(sequence[len/2] + sequence[len/2+1]) / 2 :
sequence[(len+1)/2];
// 计算标准差
// 所有数减去其平均值的平方和,再除以数组个数(或个数减一,即变异数)再把所得值开根号
let stdDev = Math.sqrt(numbers.map(n=> (n-avg) * (n-avg)).reduce(sum) / len);
return {
max,
min,
avg: avg.toFixed(digit),
mid: parseFloat(mid).toFixed(digit),
stdDev : stdDev.toFixed(digit)
}
}
版权声明:本文为weixin_55846296原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。