提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档


提示：以下是本篇文章正文内容，下面案例可供参考


一、01背包是什么？

给定n种物品，每种物品都有重量w,和价值v,，每种物品只有一个，背包容量为W。求解在不超过背包容量的情况下，将哪些物品放入背包，使背包中的物品价值之和最大。每种物品只有一个，要么不放入（0)，要么放入(1)，因此称之为01背包。

二、解题步骤

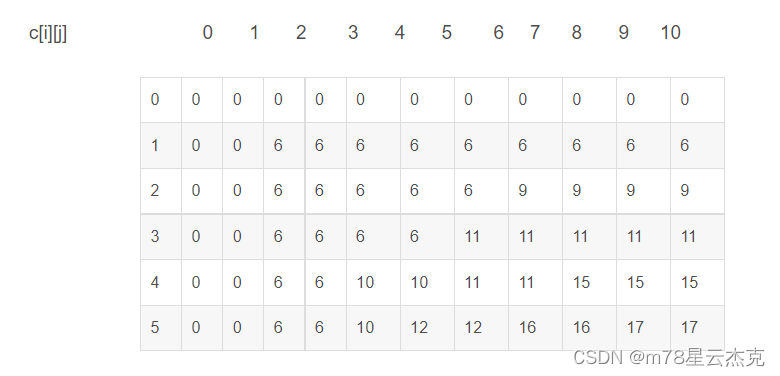
(1）确定状态。c[i]表示前i种物品放入容量为j的背包中获得的最大价值。

(2）划分阶段。第i阶段处理第i种物品，第i-1阶段处理第i-1种物品。当处理第i种物品时，前i-1种物品己处理完毕，只需考虑第i-1阶段向第阶段的转移。（

不放入背包：问题转化为“将前i-1种物品放入容量为j的背包中获得的最大价值”，最大价值为c[i-1][j]。

放入背包：问题转化为“将前i-1种物品放入容量为j-w[i]的背包中获得的最大价值e[i-1][j-w[i]]”，加上第i种物品的价值v[i]，命c[i-1][j-w[i]]+v[i]。

）

(3）决策选择。若背包容量不足，则不能放入，价值仍为前i-1种物品处理后的结果;若背包容量充足，则考察放入、不放入哪种情况获得的价值更大。

状态转移方程：

(4）边界条件。c[0][]=0，c[i][0]=0，i=0,…n，j=0,…W

(5）求解目标。c[n][W]。

三、代码及实例：

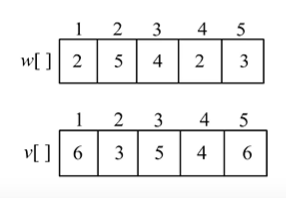
题目：有5个物品，背包的容量为10。求放入背包的最大价值？

代码如下：

public class test {

	public static void main(String[] args) {
		// TODO 自动生成的方法存根
		int[] w= {2,5,4,2,3};
		int[] v= {6,3,5,4,6};
		System.out.println(bagkiller(w,v,10));
	}
	public static int bagkiller(int[] w,int[] v,int n) {   //w[]是重量 v[]是价值  n 是背包容量
		int [][] dp=new int[w.length+1][n+1];    //初始值dp[0][0至n]和dp[0至n][0]初始值为0，因为java数组初始值全为0，所以不用特殊定义
		for (int i=1;i<=w.length;i++) {
			for (int j=1;j<=n;j++) {
				if(w[i-1]>j) {    //由于dp数组i要从1开始，所以w数组要减一，避免数组越界（dp[1]的时候w[0]）
					dp[i][j]=dp[i-1][j];
				}
				else
					dp[i][j]=Math.max(dp[i-1][j], dp[i-1][j-w[i-1]]+v[i-1]);
				}
			}
		return dp[w.length][n];
	}
}

结果：

17