这种算法可以用抽样的方法模拟任何一种分布,计算其均值、方差等特征,前提是知道该分布的密度函数,但不必知道其分布函数。
引例一
先来看一个简单的小例子,即给出一些均匀分布的随机数,我们可以模拟指数分布。
模拟过程如下:
首先生成一些[0,1]均匀分布的随机数,可以看作是随机生成的指数分布的概率密度,因此代入指数分布函数(cdf)的反函数,即可求出服从指数分布的随机数。可以再生成一些真正的指数分布随机数,和我们人造的随机数进行比较,比较方式是画出其频率分布直方图,可以看出其分布相似且近似指数分布。
par(mfrow=c(1,2))
x = rexp(1000,rate = 3) #指数分布随机数
xu = runif(1000,0,1) #均匀分布随机数
xe = -log(1-xu)/3 #均匀随机数生成的指数随机数
hist(x)
hist(xe)
plot(density(x))
plot(density(xe))

引例二
然而对于cdf的反函数比较复杂的分布,这种方法就行不通了,因此我们采用另一种方法,称为拒绝接受的算法:
已知目标分布的密度函数pdf:
f
y
(
x
)
f_y(x)
f
y
(
x
)
,我们首先生成[0,1]上均匀分布的随机数u,以及一个与目标分布有相同定义域且形态相似的分布
f
v
(
x
)
f_v(x)
f
v
(
x
)
,接下来将分布
f
v
(
x
)
f_v(x)
f
v
(
x
)
乘以一个大于1的数M,变为M
f
v
(
x
)
f_v(x)
f
v
(
x
)
,可以完全包含目标分布。运用均匀分布生成伯努利分布的思想,确定M
f
v
(
x
)
f_v(x)
f
v
(
x
)
中在目标分布里面的点,这实际上是一种拒绝接受的策略:
P
(
x
<
X
∣
u
<
f
y
(
x
)
/
M
∗
f
v
(
x
)
)
P(x<X | u< f_y(x)/M*f_v(x))
P
(
x
<
X
∣
u
<
f
y
(
x
)
/
M
∗
f
v
(
x
)
)
即为目标分布的概率密度。即我们保留在
f
y
(
x
)
f_y(x)
f
y
(
x
)
中的点,图中的阴影部分即为拒绝域。
(图中为二维展示,事实上对于高维复杂的目标分布,我们只能知道其概率密度函数,却并不能画出其形状)

这种抽样方法的效率实际上依赖于M的取值和这两种分布的相似性,M越大,相似性越低,则拒绝域越大,抽样效率越低。
因此我们需要寻找一种更普适的、效率更高的抽样方法,即Metropolis Hasting算法。
Metropolis Hasting算法
这个算法是Metropolis在二战时为了计算原子弹最佳引爆条件而发明的,由于这个算法具有一般性,被发表出来成为了统计学领域的核心算法。而后Hasting对算法中的一些缺陷做出改进,因此现在的整个算法被称为Metropolis Hasting算法。算法中运用到了马尔科夫-蒙特卡罗。
蒙特卡罗(Monte Carlo)是一种重复的实验,通过不断的重复实验可以得到一些特性,最后把这些特性进行汇总。马尔科夫链(Markov chain)是不断用随机过程实现这种模拟。马尔科夫和蒙特卡罗可以分开使用,但现在流行两个加在一起使用。为了后续展开,我们先对马尔科夫链进行一些深入了解。
马尔科夫链(Markov chain)
马尔科夫链是一个随机过程,其当前的状态只与上一个状态有关:
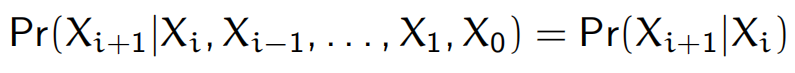
两个状态i,j之间有一个转移概率,记为
p
i
,
j
p_{i,j}
p
i
,
j
将其写成矩阵形式,记为一步转移转移矩阵
P
P
P
则n步转移概率为
P
n
P^n
P
n
简单的马尔科夫过程(遍历)最后会收敛到一个平稳分布
lim
n
→
+
∞
P
n
=
Π
\lim\limits_{n\to+\infty} P^n = \Pi
n
→
+
∞
lim
P
n
=
Π
只要构造一个策略使得最后的平稳分布恰为目标分布的密度函数。我们可以去除马尔科夫链最开始的一些不稳定状态,仅保留之后收敛的状态作为目标分布的近似。
首先,我们给出一个对目标分布(p)的猜想分布(q),这个q可以是任何一种分布,这里取成正态分布。但这个猜想分布肯定是不准确的,因此我们用马尔科夫链对其做变换,使它一步步接近目标分布。
变换方法如下:每次生成的新的x记为x_new,它是由原来的x(记为x_old)生成的,可以取
x
[
n
e
w
]
∼
N
(
x
[
o
l
d
]
,
1
)
x^{[new]} \sim N(x^{[old]},1)
x
[
n
e
w
]
∼
N
(
x
[
o
l
d
]
,
1
)
,称为随机游走猜想。
随机游走(Random Walk)
可以理解为一个喝醉酒的人从酒吧出来,在街上随机向左走或向右走,走到某一个位置后停下,下一次再走就是以这个位置为中心开始随机向左走或向右走。
随机游走也可以扩展到二维空间,例如这个醉汉一出门就是个十字路口,他每次随机选择向前后左右走几步。
并不是每次生成的x_new都是有用的(即满足p(x)分布),我们必须对其做判断,这就是Metropolis Hasting算法要实现的东西。
我们希望生成的x_new能使p(x_new)越大越好,这样就能更接近目标分布,因此定义接受概率
α
\alpha
α
:
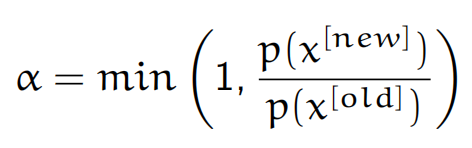
这意味着若 p(x_new)>p(x_old) 则以概率1接受 x_new,否则以p(new)/p(old) 的概率决定是否接受,若不接受则 x_old没有被更新。
以上就是Metropolis Hasting算法的内容,我们甚至不需要知道未知分布的完整概率密度,只要知道它的核即可。
应用
这里给出一个具体应用的例子:模拟一个自由度为5的t分布,给出核的表达式
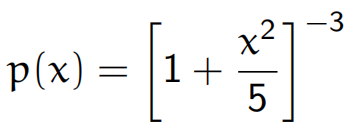
定义初始值
x
0
x_0
x
0
,q分布的方差,一共生成多少个x值(这里是110000个)
前面没有收敛的x值称为燃烧值(burn-in),可以删去,仅留下最后的100000个值,这些随机数才是满足目标分布的。
注意,如果将方差设置得很小,那么接受概率
α
\alpha
α
的值可能也很小,则应该写成对数形式。
target = function(x){(1+x^2/5)^(-3)}
random_walk = function(nn, x0, var){
n = 1
x_old = x0
A = matrix()
X = matrix()
X[1] = x_old
while (n < nn) {
x_new = rnorm(1,x_old,var)
p_old = target(x_old)
p_new = target(x_new)
a = min(1,p_new/p_old)
A[n] = a
b = rbinom(n = 1, size = 1, prob = a)
if(b==1){x_old = x_new}
X[n+1] = x_old
n = n + 1
}
X_converge = X[10001:length(X)]
result = list(A,X,X_converge)
return(result)
}
result = random_walk(110000,0,1)
检验
这里主要是检验生成的马尔科夫链是否收敛
第一种方法是画图检验,若均值和方差都很稳定则可以认为是收敛的
注意我们做的是抽样,和优化不同。优化最后会收敛到一条线,而抽样是一个区间。
可以不断改变初始值和方差来进行尝试,能发现收敛性是依赖于初始值和方差的,方差较大则收敛性不好。
X = unlist(result[2])
plot(X, pch=20, ylab = 'x', main = 'x0=0, var=1') #trace plot


第二种方法是借助ACF函数,这个函数是检验两个观测值之间的自相关性。由于整个抽样过程依赖于马尔科夫性,这种性质要求
x
n
x_n
x
n
只能与
x
n
−
1
x_{n-1}
x
n
−
1
有关,若ACF迅速下降则说明抽样较好,否则自相关性太强,抽样过程不好。
X_converge = unlist(result[3])
acf(X_converge)

上图的ACF显示自相关性很强,下图则较好

也可以用coda包中的Geweke diagnostic来进行检验。这个检验是从马尔科夫链中抽取两段,如果马尔科夫链收敛,则这两段应该有相同的均值

最后一种方法是看
α
\alpha
α
的值,一般情况下
α
\alpha
α
介于0.2到0.5之间,若 <0.1 或 >0.7 则认为抽样过程不好。