??
个人主页:
研学社的博客
????
欢迎来到本博客
❤️❤️??
?博主优势:
???
博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️
座右铭:
行百里者,半于九十。
???
本文目录如下:
???
目录

?1 概述
格子波尔兹曼模型(Lattice Boltzmann Model,LBM)是近年来兴起的一种求解偏微分方程的数值工具。目前,LBM在流体力学领域中的应用已经和传统的数值方法并驾齐驱,得到了国际上的广泛关注。LBM和传统的求解偏微分方程的数值方法的区别在于其出发点是系统的微观模型,使LBM的宏观方程与偏微分方程保持一致,并在对系统进行模拟的同时,实现对偏微分方程的求解。虽然目前LBM在图像处理领域中的应用鲜有报道,但实际上LBM在图像处理领域有着很大的应用潜力。首先,从上世纪六十年代开始,作为LBM发展前身的传统元胞自动机在图像处理领域中就已经得到广泛应用。其次,LBM继承了传统元胞自动机方法在图像处理中的优点,如算法实现简单,计算并行度高,模型稳定性好。再次,LBM是一个非常有效的数值工具,在流体力学中它被广泛用来求解各种偏微分方程。借鉴基于偏微分方程理论的图像处理模型与方法,利用LBM求解偏微分方程,可以实现包括图像去噪,图像边缘检测和图像分割在内的各种图像处理。
?
2 运行结果
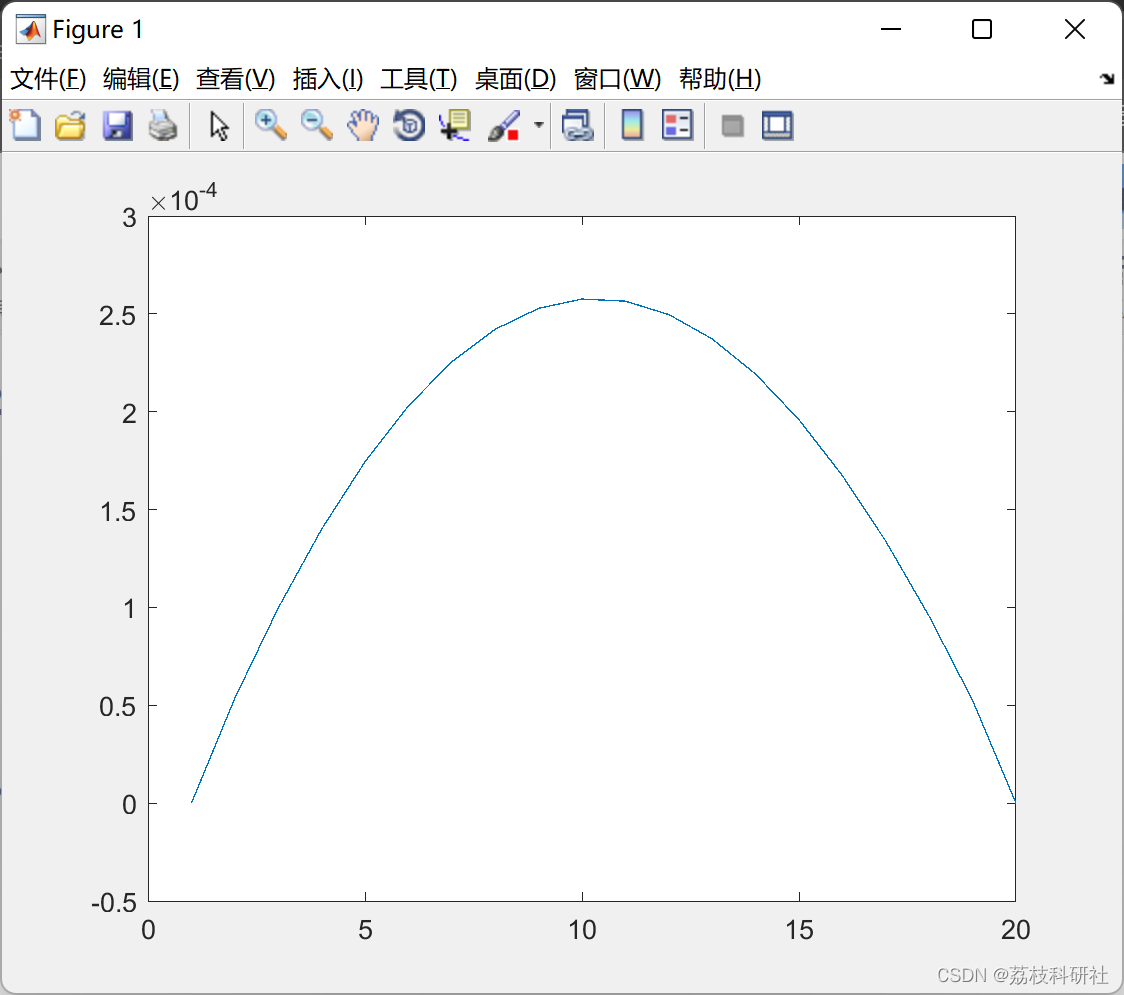
部分代码:
OMEGA=0.2;%Relaxation factor
TAU=1/OMEGA;
XMAX=20;%Mesh size in x-direction
YMAX=20;%Mesh size in y-direction
FORCING=(1.024)/YMAX^3;%Forcing term in Poiseuille equation
KVISC = ((1/OMEGA)-0.5)/3;%lattice viscosity
UX=(0.5*FORCING*YMAX*YMAX)/KVISC;%Velocity in x-direction
cx=[1 0 -1 0 1 -1 -1 1 0];%components of lattice velocities in x-direction
cy=[0 1 0 -1 1 1 -1 -1 0];%components of lattice velocities in y-direction
jx=zeros(XMAX,YMAX);%creating an array for storing momentum in x-direction
jy=zeros(XMAX,YMAX);%creating an array for storing momentum in y-direction
rho=ones(XMAX,YMAX);%creating an array for storing densities
f=zeros(XMAX,YMAX);%creating an array for storing distributions
fprop=zeros(XMAX,YMAX);%creating an array for storing propagating distributions
x=1:XMAX;
y=1:YMAX;
MAXIT=input(‘Number of iterations’);
%Initializataion of distributions
u=jx./rho;
v=jy./rho;
f(x,y,1) = (rho./9)*(1+3.*u+4.5.*u.*u-1.5.*(u.^2+v.^2));
f(x,y,2) = (rho./9)*(1+3.*v+4.5.*v.*v-1.5*(u.^2+v.^2));
f(x,y,3) = (rho./9)*(1-3.*u+4.5.*u.*u-1.5*(u.^2+v.^2));
f(x,y,4) = (rho./9)*(1-3.*v+4.5.*v.*v-1.5*(u.^2+v.^2));
f(x,y,5) = (rho./36)*(1+3.*(u+v)+4.5*(u+v).^2-1.5*(u.^2+v.^2));
f(x,y,6) = (rho./36)*(1+3.*(-u+v)+4.5*(-u+v).^2-1.5*(u.^2+v.^2));
f(x,y,7) = (rho./36)*(1-3.*(u+v)+4.5*(u+v).^2-1.5*(u.^2+v.^2));
f(x,y,8) = (rho./36)*(1+3.*(u-v)+4.5*(u-v).^2-1.5*(u.^2+v.^2));
f(x,y,9) = (4/9)*rho.*(1-1.5*(u.^2+v.^2));
%Initialization completed
%Assign first fprop to equilibrium distributions.
fprop=f;
feq=zeros(20,20,9);
for iter=1:MAXIT
u=jx./rho;
v=jy./rho;
feq(x,2:YMAX-1,1) = (rho(x,2:YMAX-1)./9).*(1+3.*u(x,2:YMAX-1)+4.5.*u(x,2:YMAX-1).*u(x,2:YMAX-1)-1.5.*(u(x,2:YMAX-1).^2+v(x,2:YMAX-1).^2));
feq(x,2:YMAX-1,2) = (rho(x,2:YMAX-1)./9).*(1+3.*v(x,2:YMAX-1)+4.5.*v(x,2:YMAX-1).*v(x,2:YMAX-1)-1.5.*(u(x,2:YMAX-1).^2+v(x,2:YMAX-1).^2));
feq(x,2:YMAX-1,3) = (rho(x,2:YMAX-1)./9).*(1-3.*u(x,2:YMAX-1)+4.5.*u(x,2:YMAX-1).*u(x,2:YMAX-1)-1.5.*(u(x,2:YMAX-1).^2+v(x,2:YMAX-1).^2));
feq(x,2:YMAX-1,4) = (rho(x,2:YMAX-1)./9).*(1-3.*v(x,2:YMAX-1)+4.5.*v(x,2:YMAX-1).*v(x,2:YMAX-1)-1.5.*(u(x,2:YMAX-1).^2+v(x,2:YMAX-1).^2));
feq(x,2:YMAX-1,5) = (rho(x,2:YMAX-1)./36).*(1+3.*(u(x,2:YMAX-1)+v(x,2:YMAX-1))+4.5*(u(x,2:YMAX-1)+v(x,2:YMAX-1)).^2-1.5*(u(x,2:YMAX-1).^2+v(x,2:YMAX-1).^2));
feq(x,2:YMAX-1,6) = (rho(x,2:YMAX-1)./36).*(1+3.*(-u(x,2:YMAX-1)+v(x,2:YMAX-1))+4.5*(-u(x,2:YMAX-1)+v(x,2:YMAX-1)).^2-1.5*(u(x,2:YMAX-1).^2+v(x,2:YMAX-1).^2));
feq(x,2:YMAX-1,7) = (rho(x,2:YMAX-1)./36).*(1-3.*(u(x,2:YMAX-1)+v(x,2:YMAX-1))+4.5*(u(x,2:YMAX-1)+v(x,2:YMAX-1)).^2-1.5*(u(x,2:YMAX-1).^2+v(x,2:YMAX-1).^2));
feq(x,2:YMAX-1,8) = (rho(x,2:YMAX-1)./36).*(1+3.*(u(x,2:YMAX-1)-v(x,2:YMAX-1))+4.5*(u(x,2:YMAX-1)-v(x,2:YMAX-1)).^2-1.5*(u(x,2:YMAX-1).^2+v(x,2:YMAX-1).^2));
feq(x,2:YMAX-1,9) = ((4/9)*rho(x,2:YMAX-1)).*(1-1.5*(u(x,2:YMAX-1).^2+v(x,2:YMAX-1).^2));
%propagating distributions fprop by applying kinetic equation.
?
3 Matlab代码实现
?4
参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]陈玉. 格子波尔兹曼模型及其在图像处理中的应用研究[D].上海大学,2008.