一、灰色系统含义
1、白色系统
• 具有较
充足的信息量
,其
发展变化规律明显
,定量描述较方便,结构与参数较具体,称之为白色系统;
2、灰色系统
• 无法建立客观的物理原型,其作用原理亦不明确,内部因素难以辨识或之间关系隐蔽,对其定量描述难度较大,带来建立模型的困难。系统内部特性部分已知的系统称之为灰色系统;
3、黑色系统
• 一个系统的内部特性
全部未知
,称之为黑色系统。
相对的,绝对的白色或黑色系统很少。
4、白化
• 灰色系统理论将随机量看作是在一定范围内变化的灰色量,按适当的办法将原始数据进行处理,将灰色数变换为生成数,从生成数进而得到规律性较强的生成函数。
• 灰色系统理论的量化基础是生成数,从而突破了概率统计的局限性,使其结果不再是过去依据大量数据得到的经验性的统计规律,而是现实性的生成律。
• 这种使灰色系统变得尽量清晰明了的过程被称为白化。
5、何时能用灰色模型?
当题目中的
数据量少、无明显规律、短期预测
时,一般可以使用灰色预测模型。
二、构造灰色预测模型需要明确几个概念
1、引言
我们得到数据之后可以先把图像绘图,一般来说此时绘制的这个图像是看不出什么规律的,很
难去预测
以后的值。(这是
灰色系统本身决定
)。
那么问题来了,既然
直接看没有规律性
,那么我们就要人为去
选择
合适的
方法制造规律
。
(一切灰色序列都能通过某种生成弱化其随机性,显现其规律性。)
数据生成的常用方式有
累加生成、累减生成和加权累加生成
。
其中经常用的方式便是
累加生成
。
2、累加生成

• 累加生成可使非负的摆动与非摆动的数列或任意无规律性的数列转化为非减的数列。
• 有些实际问题的数列中有负数,为避免出现正负抵消这种信息损失的现象, 我们可以先进行移轴,然后再做累加生成。
3、累减生成
还原累加生成的办法是累减生成。
对原始数列依次做前后两数据相减的运算过程叫累减生成,记作IAGO。
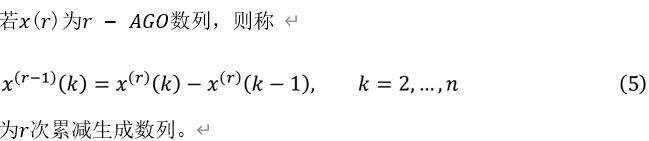
4、均值生成


5、灰色模型GM
灰色系统理论是基于关联空间、光滑离散函数等概念定义灰导数与灰微分方 程,进而用离散数据列建立微分方程形式的动态模型,由于这是本征灰色系 统的基本模型,而且模型是近似的、非唯一的,故这种模型为灰色模型,记 为GM(Grey Model). 灰色模型是利用离散随机数经过生成变为随机性被显著削弱而且较有规律的 生成数,建立起的微分方程形式的模型,这样便于对其变化过程进行研究和 描述。
•
GM(1,1)
表示模型是
1阶方程
,且只含
1个变量
的灰色模型; •
GM(1, ?)
表示模型是
1阶方程
,包含有
?个变量
的灰色模型。
6、灰色预测
• 利用??模型对系统行为特征的发展变化规律进行估计预测,同时也对行为特 征的异常情况发生的时刻进行估计计算,对在特定时区内发生事件的未来时 间分布情况做出研究等。 • 实质上是将
“随机过程”当作“灰色过程”
,
“随机变量”当作“灰变量”
,并主要以灰 色系统理论中的
GM(1,1)模型
来进行处理。 • 依据目前已有的数据对未来的发展趋势做出预测分析。
灰色预测的具体操作将在以后的博客进行介绍