前言
虽然网上也有很多关于方差分析的介绍,但是我还是想结合自己在学校所学的统计学专业知识以及网上的一些优秀文档做一个笔记整理,不为别的,只为以后用到这方面知识的时候有笔记可查,分享到博客也是为了和大家一起学习探究,无其他过分的想法,谢谢各位。
PS:由于markdown编辑器不支持数学公式的直接复制,所以只能先在Word文档编辑好,然后以插图的形式放进来,因此在文章发现有文档的插图请不要奇怪,正常操作 [笑脸]
1 方差分析概述
1.1 方差分析的作用
为了进行两组以上均值的比较,通常可以使用方差分析的方法,也就是说方差分析用于两个及两个以上样本均数差别的显著性检验。在诸多领域的数量分析研究中,找到众多影响因素中重要的影响因素是非常重要的。比如:在农业生产中,我们总是希望在尽量少的投入成本下得到较高的农作物产物。这就需要首先分析农作物的产量究竟受到哪些因素的影响。有许多因素会影响农作物的产量,如种子的品种、施肥、气候、地域等,他们都会给农作物的产量带来或多或少的影响。如果我们能够掌握在众多的影响因素中,哪些因素对农作物的产量起了主要的、关键性的作用,我们就可以根据实际情况对这些关键因素加以控制。
1.2 影响因素分类
受不同因素的影响,研究所得的数据会不同。造成结果差异的原因可分成两类:一类是不可控的随机因素的影响,这是人为很难控制的一类影响因素,称为随机变量,在很多情况下,随机因素指的是实验过程中的抽样误差;另一类是研究中人为施加的可控因素对结果的影响,称为控制变量。
1.3 方差分析的基本思想
方差分析的基本思想是:通过分析研究不同变量的变异对总变异的贡献大小,确定控制变量对研究结果影响力的大小。通过方差分析,分析不同水平的控制变量是否对结果产生了显著影响。如果控制变量的不同水平对结果产生了显著影响,那么它和随机变量共同作用,必然使结果有显著的变化;如果控制变量的不同水平对结果没有显著的影响,那么结果的变化主要由随机变量起作用,和控制变量关系不大。
1.4 方差分析的分类
根据控制变量的个数,可以将方差分析分成单因素方差分析、多因素方差分析以及协方差分析。单因素方差分析的控制变量只有一个(但一个控制变量可以有多个观察水平),多因素方差分析的控制变量有多个,而协方差分析的控制因素可以是单因素或者多因素,不同的是协方差分析存在协变量(协变量一般为连续型定量变量)。
2 单因素方差分析
2.1 单因素方差分析统计原理
定义:单因素方差分析测试某一个控制变量的不同水平是否给观察变量造成了显著差异和变动。例如,培训是否给学生成绩造成了显著影响;不同地区的考生成绩是否有显著的差异等。


建立原假设H0:控制变量不同水平下观测变量各总体的均值无显著差异。计算检验统计量F值和其相伴概率值,如果相伴概率值小于显著性水平α,则拒绝原假设,认为控制变量不同水平下各总体均值有显著差异;反之,则认为控制变量不同水平下各总体均值没有显著差异。
2.2 实例与SPSS实现过程
研究不同组别的数学成绩是否有显著差异,其三组学生的数学成绩如下:
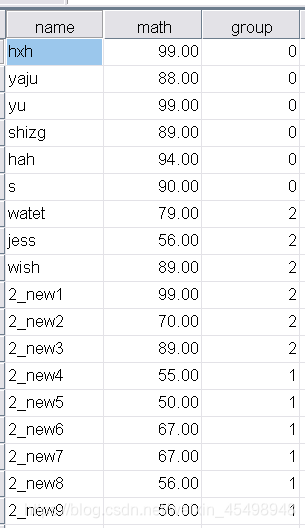
在SPSS中操作步骤如下:(1)单击菜单Analyze->Compare means->One-Way ANOVA,出现对话框如图1所示:
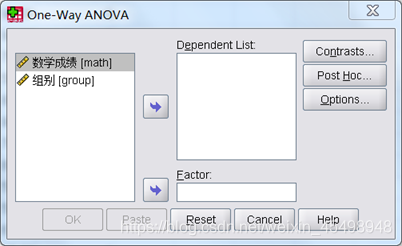
图1
(2)将观察变量选择到Dependent List框。(3)将控制变量选择到Factor框。控制变量有几个不同的取值表示控制变量有几个水平。(4)单击Options按钮,如图2所示:

图2
勾选Statistics栏的Homogeneity of variance test(方差齐性检验)选项、means plot选项、Missing Value栏选择Exclude cagses analysis by analysis(按分析顺序排除个案)选项。Statistics栏其他选项含义如下:Descriptive选项表示因变量的有关统计量值,Fixed and random effects选项包含标准差、标准误差、95%的置信等统计,Brown-Forsythe选项表示均值相等假设Brown-Forsythe的统计量,Welch表示均值相等假设的Welch统计量。由于方差分析的前提是各水平下的总体服从正态分布并且方差相等,因此有必要先对方差进行齐性检验(Homogeneity of Variance),即对控制变量不同水平下各观测变量不同总体方差是否相等进行分析,其原假设为各水平下观察变量总体方差无显著差异,实现思路同两独立样本t检验中的方差齐性检验。(5)单击Post Hoc按钮,弹出Post Hoc Multiple Comparisons(多重比较)对话框,如图3所示:
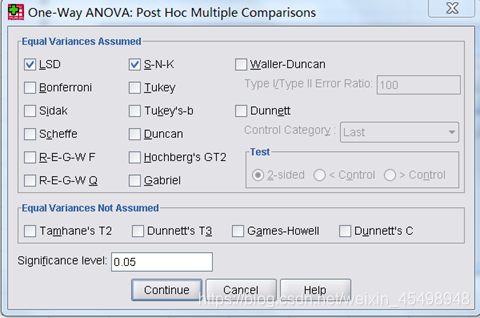
图3
勾选Equal Variances Assumed(假设方差相等)栏的LSD选项、S-N-K选项(其中各选项的含义如下:LSD选项用于t检验完成各组间的配对比较,Bonferroni选项用于设置每一试验对的误差率控制整个误差率,Sidak选项用于基于t统计量的配对多重比较检验,Scheffe选项用于F分布对所有可能的组合进行同时进入的配对比较,R-E-G-W F选项用于F检验的多重递减程序,R-E-G-W Q选项用于学生氏极差分布的多重递减程序,S-N-K选项用于学生氏极差分布做出的均值的所有的配对比较,Tukey选项用于学生氏极差分布做出的组间的所有的配对比较,Tukey’s-b选项用于学生氏极差分布做出的组间的配对比较,Duncan选项用于按序逐步比较的方法做出的配对比较,Hochberg’s GT2选项用于学生氏最大模分布进行多重比较和极差检验,Waller-Duncan选项用于基于t统计量使用贝叶斯逼近的多重比较检验法,Dunnett选项用于多重配对比较的t检验法),另外Equal Variances Not Assumed(假设方差不相等)栏的Tamhane’sT2选项用于基于t检验的一种较为保守的配对比较检验法、Dunnett’T3选项用于基于学生氏最大模分布的配对比较检验法、Game-Howell选项用于一种较为随意的配对比较检验法、Dunnett’s C选项用于基于学生氏极差分布的配对比较检验法,最后将Signification level框的值(多重比较检验法的显著性水平)设置为0.05。SPSS提供的多重比较检验的方法比较多,有些方法适用在方差相等的条件下,有些适用在方差不相等的条件下,其中LSD方法适用于各总体方差相等的情况,特点是比较灵敏;Tukey方法和S-N-K方法适用于各水平下观测变量个数相等的情况;Scheffe方法比Tukey方法不灵敏。(6)单击Contrasts(对比)按钮,勾选Polynomial(多项式)选项,Degree(水平)下拉框选择Linear(线性),如图4所示,然后单击Continue按钮回到One-Way ANOVA对话框。
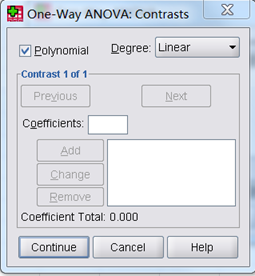
图4
在其他检验中(Contrasts选项)有:
(1)先验对比检验:如果发现某些水平与另一些水平的均值差距显著,就可以进一步比较这两组总的均值是否存在显著差异,在检验中,SPSS根据用户确定的各均值的系数,再对其线性组合进行检验,来判断各相似性子集间均值的差异程度;(2)趋势检验:当控制变量为定序变量时,趋势检验能够分析随着控制变量水平的变化,观测变量值变化的总体趋势是怎样的。
Contrasts选项(对比选项)用来实现先验对比检验和趋势检验:(1)如果进行趋势检验,则应选择Polynomial选项,然后在Degree的下拉框中选择趋势检验的方法,其中Linear表示线性趋势检验、Quadratic表示进行二次多项式检验、Cubic表示进行三次多项式检验,4th和5th表示进行四次和五次多项式检验;(2)如果进行先验对比检验,则应在Coefficients后依次输入系数 ,并确保 =0,应注意系数输入的顺序,它将分别与控制变量的水平值相对应。
完成所有按钮的设置后,单击One-Way ANOVA对话框的OK按钮得到以下结果:

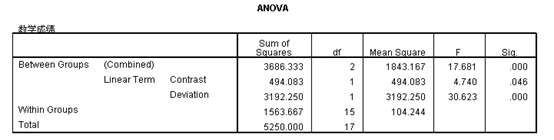
单因素方差分析—结果1
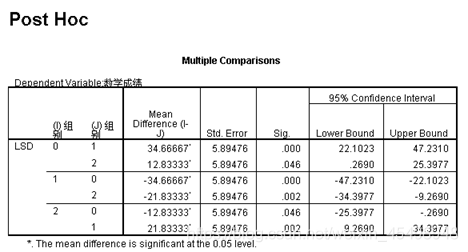
单因素方差分析—结果2
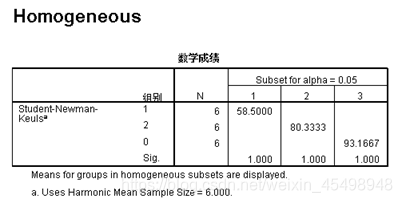
单因素方差分析—结果3
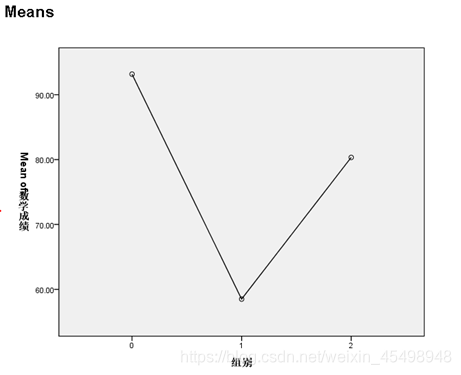
单因素方差分析—结果4

3 多因素方差分析
3.1 多因素方差分析原理
多因素方差分析中的控制变量在两个或两个以上,它的研究目的是要分析多个控制变量的作用、多个控制变量的交互作用以及其他随机变量是否对结果产生了显著影响。
多因素方差分析不仅需要分析多个控制变量独立作用对观察变量的影响,还要分析多个控制变量交互作用对观察变量的影响,及其他随机变量对结果的影响,因此,它需要将观察变量总的离差平方和分解为3个部分:(1)多个控制变量单独作用引起的平方和;(2)多个控制变量交互作用引起的离差平方和;(3)其他随机因素引起的离差平方和。


3.2 实例与SPSS实现过程
研究三组不同性别学生的数学成绩是否有显著差异,其数学成绩数据如下:
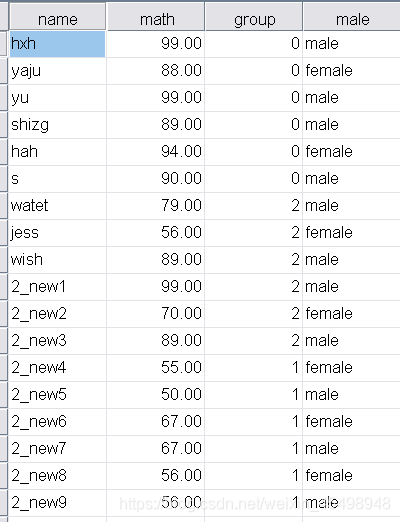
在SPSS中操作步骤如下:(1)单击菜单Analyze->General Linear Model->Univariate(这里说明一下,虽然Univariate意为单变量,但其实该按钮可以实现多因素方差分析),弹出Univariate对话框,如图5所示:
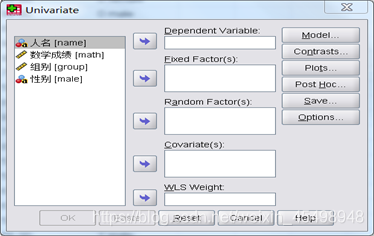
图5
将数学成绩变量选入Dependent Variable(因变量)方框、将性别变量和组别变量选入Fixed Factor(控制变量)方框,单击Option按钮进入Univariate:Option对话框,如图6所示:
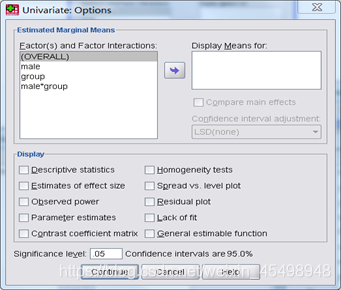
图6
勾选Display栏的Homogeneity tests选项(齐次检验),单击Continue按钮回到Univariate对话框;接着单击Post Hoc按钮进入Post Hoc Multiple Comparisons for Observed Means(观察值均值多重比较)对话框,如图7所示:
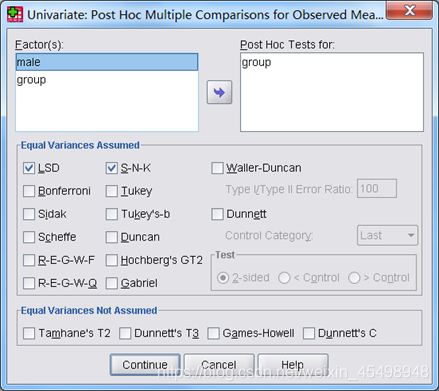
图7
将因素变量group选入Post Hoc Tests for(事后多重检验)栏,勾选Equal Variances Assumed(假设方差相等)栏的LSD选项和S-N-K选项,单击continue回到Univariate对话框;接着单击Model按钮,进入Univariate:Model对话框,Specify Model(指定模型)栏选择Full factorial(全因子)选项,其他保持默认设置,单击Continue按钮回到Univariate对话框;
接着单击Contrasts按钮,进入Univariate:Contrasts(对比)对话框,如图8所示:
图8
选中male因素,然后在Change Contrast栏的Contrast下拉选项选择Simple,单击Change按钮将因素的None状态改为Simple状态,对group因素执行相同操作后在Reference Category(参考类别)项选择Last,单击continue回到Univariate对话框;接着单击Plots按钮,进入Univariate:Profile Plots(绘图)对话框,如图9所示:
图9
将group因素选入Horizontal Axis(横坐标轴)栏、male因素选入Separate Lines(分离线)栏,然后单击plots项的Add按钮,接着单击Continue按钮回到Univariate对话框。
最后单击OK按钮得到以下结果:
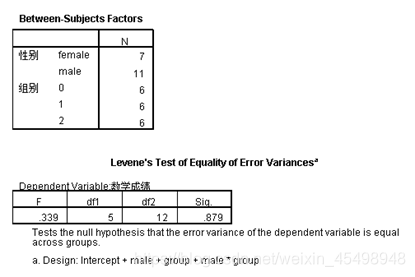
多因素方差分析—结果1
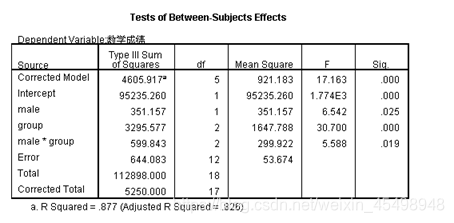
多因素方差分析—结果2
多因素方差分析—结果3
多因素方差分析—结果4
多因素方差分析—结果5
多因素方差分析—结果6
3.3 结果解释
(1)多因素方差分析—结果1
的第二个表是检验原假设为因变量组间误差方差相等的Levene检验(即方差齐性检验),其中误差方差是由常数项、性别(male)因素项、组别(group)项、以及性别和组别的交互项组成的,从结果表我们可以看到F统计量的值为0.339,其伴随概率p值为0.879,大于显著性水平α=0.05,说明没有充分的理由拒绝原假设,即方差齐性检验通过,这是能够进行多因素方差分析的一个前提假设。
(2)多因素方差分析—结果2
是各主体间效应的检验(Tests of Between—Subjects Effects)结果:首先看到模型修正项(Corrected Model)的F统计量值为17.163,其伴随概率p值为0 < 显著性水平α=0.05,说明拒绝原假设,即多个控制变量的不同水平下,各总体均值存在显著差异;然后看到性别变量主效应、组别变量主效应以及性别与组别的交互效应的F统计量的伴随概率p值均小于显著性水平α=0.05,即均拒绝原假设,说明性别控制变量的不同水平、组别控制变量的不同水平、以及性别控制变量和组别控制变量各个水平的交互作用对观察变量均产生了显著影响。
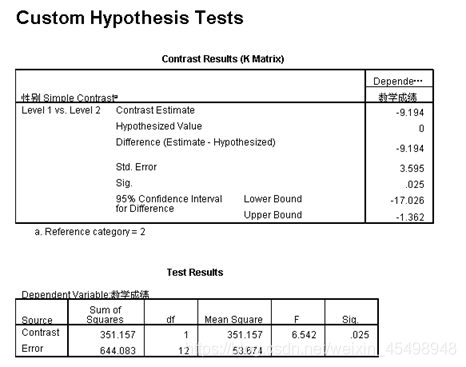
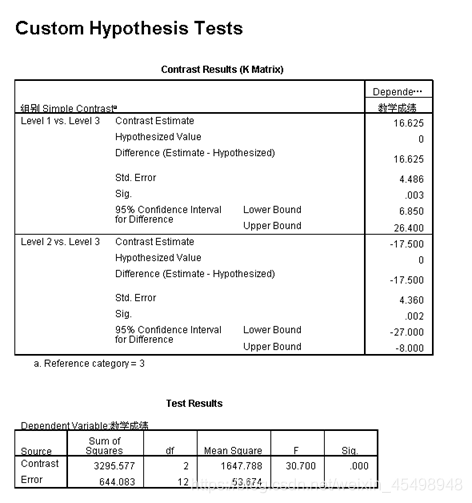
(3)多因素方差分析—结果3
是性别变量和组别变量各自不同水平两两简单对比的检验结果:首先看到性别简单对比(Simple Contrast)的对比结果(Contrast Results)K矩阵(K Matrix)和检验结果(Test Result),性别变量有两个水平,其对比检验结果的F统计量值为6.542,对应的伴随概率p值为0.025 < 显著性水平α=0.05,说明拒绝原假设,即性别变量的不同水平的观测值存在显著性差异;第二部分是组别简单对比的对比结果k矩阵和检验结果,组别变量有三个水平,其两两对比结果和对比检验结果的F统计量的伴随概率p值均小于显著性水平α=0.05,说明拒绝原假设,即性别变量的不同水平的观测值存在显著性差异。
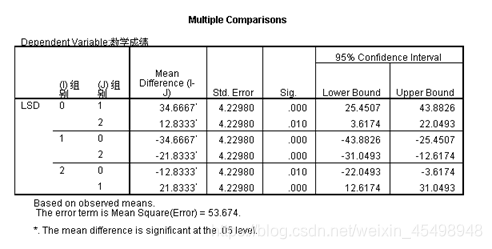
(4)多因素方差分析—结果4
是基于观察到的均值的多重比较结果,可以看到组别0、组别1、组别2的两两比较的p值均小于显著性水平α=0.05,说明均拒绝原假设,即不同组别之间存在显著性差异。
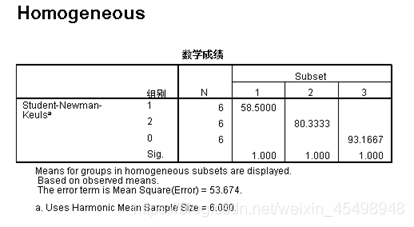
(5)多因素方差分析—结果5
是学生氏极差分布做出的均值的所有的配对比较结果,显示的是每个组的平均值,可以看到组别为0的数学成绩平均值是最高的,为93.1667。
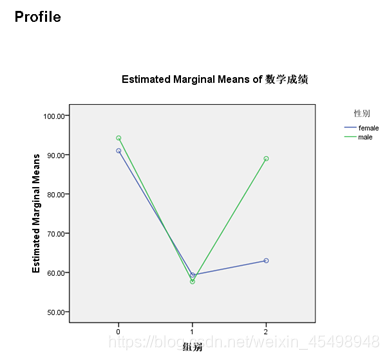
(6)多因素方差分析—结果6
是各个组别在不同性别下的数学成绩边际均值的估计结果,可以看到在男生和女生的不同组别中,其数据成绩平均值是有显著差异的;另外也可以看到组别为0的男生的数学成绩平均值要比女生的要高一点,组别为1的男生和女生的数学成绩平均值比较接近,组别为2的男生的数学成绩平均值要远高于女生的。从结果6也进一步验证了前面的几个结果是正确有效的。
4 协方差分析
4.1 协方差分析原理
协方差分析是将那些很难控制的因素作为协变量,在排除协变量影响的条件下,分析控制变量对观察变量的影响,从而更加准确地对控制变量进行评价。
协方差分析要求协变量应是连续数值型,多个协变量间相互独立,且与控制变量之间也没有交互影响。

统计量的伴随概率小于或等于显著性水平α,则说明控制变量的不同水平对观察变量产生了显著影响;如果协变量的F统计量的伴随概率小于或等于显著性水平α,则说明协变量的不同水平对观察变量产生了显著影响;反之均没有显著影响。
4.2 实例与SPSS实现过程
在已知入学数学成绩情况下研究不同组别学生的数学成绩是否有显著差异,其数据如下:
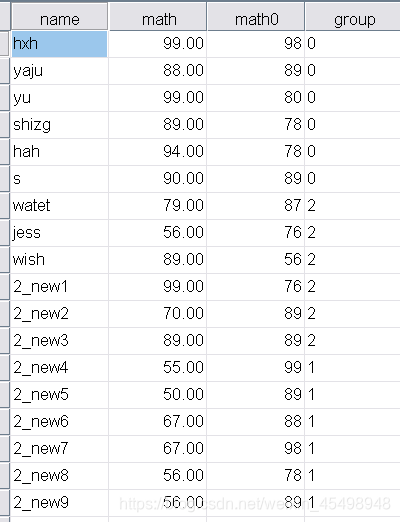
在SPSS中操作步骤如下:(1)单击菜单Analyze->General Linear Model->Univariate,弹出Univariate对话框,将数学成绩变量选入Dependent Variable(因变量)方框、将组别变量选入Fixed Factor(控制变量)方框、将入学成绩变量选入Covariate(协方差)方框,如图10所示:
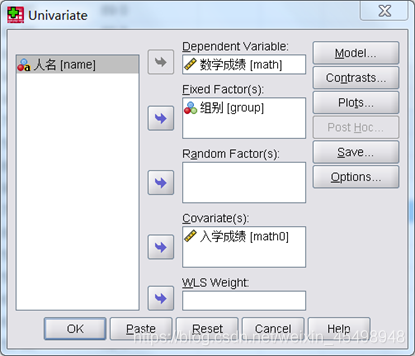
图10
由于前面已经对数学成绩进行了详细的单因素方差分析,因此为了避免不必要的重复,其他按钮不做选择,直接单击OK按钮得到以下结果:
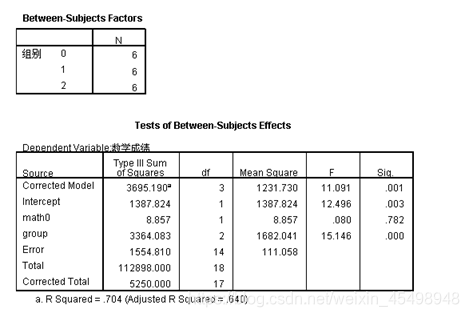
协方差分析结果
4.2 结果解释
从协方差分析的结果可以看到,协变量math0(入学成绩)的F统计量值为0.080,其伴随概率p值为0.782,大于显著性水平α=0.05,说明没有充分的理由拒绝原假设,即协变量的不同水平对观察变量没有产生显著的影响,也就是说入学成绩的高低对本次的数学考试成绩没有表现显著的影响。
SPSS操作小结:单因素方差分析主要用“Analysis”的“Compare Means”菜单下的“One—Way ANOVA”子菜单实现;多因素方差分析和协方差分析都是在“Analysis”下“General Linear Model”菜单下的“Univariate”子菜单实现的。