背景:两个天线分别坐落在两个山头上(或者其他什么地方均可,中间要保证无阻碍物),它们的波束角度都很小,大概为一度,且相距很远(几十公里),无法直接用望远镜观察位置来手动调整,因此需要通过计算调整各自的方位和仰角。两个点的经纬度和海拔均为已知条件。
首先,地球并不是完美的球体,它更接近一个两极比赤道更扁的椭球。查阅资料可得,赤道半径约为6378137米,而极半径约为6356752米,中间大概相差了22000米,因此其造成的误差已经无法忽略。对于这种情况,即使两个点的海拔一样高,在实际空间上也会有一定的高度差,会需要仰角的小幅度偏移。
我的思路:
第一步,
将经纬度和海拔转化成常用的笛卡尔坐标(xyz),这样计算起来比较熟悉和方便。通过对椭球中任意一个子午面的分析可得出换算公式:
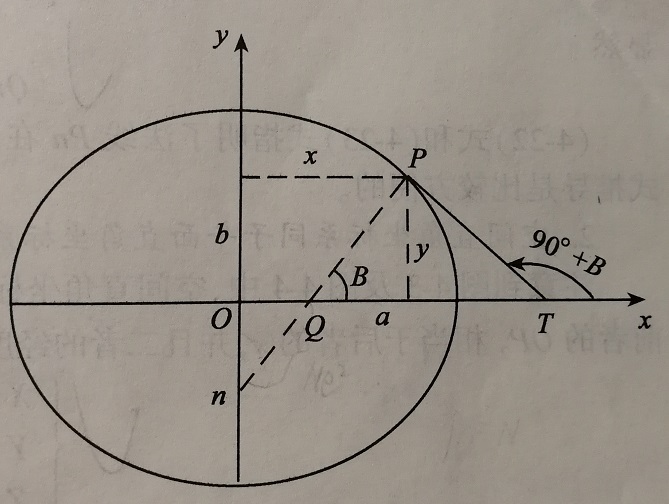
图中的y对应笛卡尔坐标系内P点的z轴,x是坐标系内P点投影向量在(x,y)与原点之间连接的线段。原理类似于球体极坐标转换成直角坐标系,根据勾股定理等可推出:
P(x) = ( N + 海拔 ) .* cos( 纬度) .* cos( 经度)
P(y) = ( N + 海拔 ) .* cos( 纬度) .* sin( 经度 )
P(z)= ( ( 1.0 – e2) .* N + 海拔 ) .* sin( 纬度 )
其中e2 = (a^2-b^2)/(a^2)
W ^2 =(1.0-e2*((sin(纬度))^2)) (这是一个常用的辅助函数,了解即可)
N = a/W;
根据这样的思路即可给出代码:
clear;
clc;
%%
%从椭球坐标(经纬度和海拔)转化成笛卡尔坐标
plh = [30.76,104.08,503.67;
30.58,104.08,503.67]; %随便给两个点的坐标,分别对应纬度经度和海拔
lat = plh(:,1)*pi/180; %latitude
lon = plh(:,2)*pi/180; %longitude
hgt = plh(:,3); %altitude
a = 6378137.0;
b = 6356752.3;
if abs(lat) > pi/2 | abs(lon) > 2*pi
warning( 'In plh2xyz(), the input latitude and/or longitude may not be in units of radians.' );
end
e2 = (a^2-b^2)/(a^2);
W = sqrt(1.0-e2*((sin(lat)).^2));
N = a./W;
pos(:,1) = ( N + hgt ) .* cos( lat ) .* cos( lon ); %x
pos(:,2) = ( N + hgt ) .* cos( lat ) .* sin( lon ); %y
pos(:,3) = ( ( 1.0 - e2 ) .* N + hgt ) .* sin( lat ); %z
Raim=sqrt(pos(:,1).^2+pos(:,2).^2+pos(:,3).^2);
pos
这样得到的pos就是一个3×2的矩阵,包含了两个点的xyz坐标。
第二步
,分别计算各自的仰角:
仰角很容易理解,如果是P0对P1点的仰角,可以看成是向量P0P1和P0点对应的椭球切面的夹角。那么只要计算出平面的法向量和向量P0P1的夹角,再用90°减去它即可。然后P1对P0的仰角同理。
根据这个思路,可以写出如下代码:
%%
%求任意一点P0(x0,y0,z0)对于点P1(x1,y1,z1)的仰角w1
%过P0点的切平面:x0*x/a^2+y0*y/a^2+z0*z/b^2-1=0
%过P0P1的直线:(x-x0)/(x1-x0)=(y-y0)/(y1-y0)=(z-z0)/(z1-z0)
x0=pos(1,1);y0=pos(1,2);z0=pos(1,3);
x1=pos(2,1);y1=pos(2,2);z1=pos(2,3);
upmn=(x1-x0)*x0/a^2+(y1-y0)*y0/a^2+(z1-z0)*z0/b^2;
downmn=sqrt(((x1-x0).^2+(y1-y0).^2+(z1-z0).^2)*((x0^2+y0^2)/a^4+z0^2/b^4));
if pos(1,3)>=pos(2,3)
w1=90-acosd(upmn/downmn);
else
w1=acosd(upmn/downmn)-90;
end
w1
需要注意的是,因为在P0和P1两个点上,它们各自的切面斜率不同,因此两个点的仰角绝对值有细微差别,并且因为方向一定是相反的(一个向上一个向下),所以得到的数值一个是正数一个是负数(要么就都是0)。
第三步
,计算各自的方向角(如:北偏东45°):
根据这个思路,可以写出下列代码:
%%
%调整方向角度w2
P1OC=acosd(abs(z1)/sqrt(x1^2+y1^2+z1^2));
EOF=plh(2,2)-plh(1,2);
P0OP1=acosd((x0*x1+y0*y1+z0*z1)/sqrt((x0^2+y0^2+z0^2)*(x1^2+y1^2+z1^2)));
C0P0P1=asind(sind(P1OC)*sind(EOF)/sind(P0OP1));
w2=abs(C0P0P1);
if plh(2,1)>=plh(1,1) & plh(2,2)>=plh(1,2)
ww=char('The azimuth is from North to East,degree is', num2str(w2));
elseif plh(2,1)>=plh(1,1) & plh(2,2)<plh(1,2)
ww=char('The azimuth is from North to West,degree is', num2str(w2));
elseif plh(2,1)<plh(1,1) & plh(2,2)<plh(1,2)
ww=char('The azimuth is from South to West,degree is', num2str(w2));
else
ww=char('The azimuth is from South to East,degree is', num2str(w2));
end
w2 %方位角w2
ww %打印指导:从南(北)向东(西)转向这样之后,天线的水平转向角即可确定。至此,天线的波束理论上即可相互连接,只需要在之后做一些较准即可。
附上运行结果:
以两个点P0(30.76,104.08,1503.67)和P1(30.58,104.04,503.67)举例(分别是纬度,经度和海拔):
结果如下:
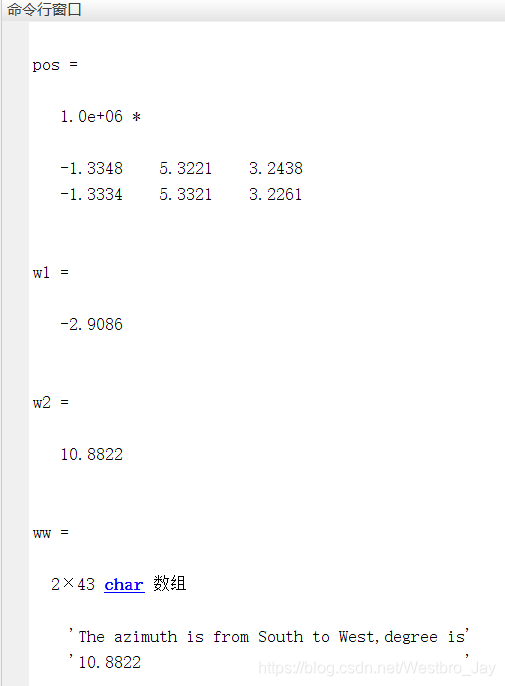
如图所示,P0对P1的仰角为w1=-2.9086°,P0对P1的方位角为S to W,w2=10.8822°,验证成功。