一、为什么要进行
我们知道,在数学建模中对问题作出一些必要的假设是非常重要的,而假设一般指的是问题有一定影响的因素但没法具体的衡量或预测,因此往往将其设为常量或者不予考虑等,但很少能保证这些假设都是完全正确的。因此我们需要考虑所得结果对每一条假设的敏感程度。这种灵敏性分析是数学建模中的一个重要方面。具体内容与所用的建模方法有关,但也并不是对每条建设都要进行灵敏度测试,所测试的往往是不能准确测量或计算的参数。
二、例子引入
案例说明:一头牛重200斤,每天增重5斤,饲料每天花费45元。牛的市场价是每斤65元,但目前行情不好,每天下降1元,求出这头牛的最佳销售时间。
这是一个很简单的单变量优化问题。求这头牛的最佳销售时间,就是求卖出价格最高的时间,为了求出这个时间,我们假设:销售时间
t
t
t
,牛的重量
w
w
w
,牛的价格
p
p
p
,饲料花费
C
C
C
,卖出牛的收益
R
R
R
,净收益
P
P
P
于是有,
P
=
R
−
C
P=R-C
P
=
R
−
C
,其中,
R
=
P
∗
w
R=P*w
R
=
P
∗
w
,
C
=
45
t
C=45t
C
=
45
t
,即得到净收益模型如下:
P
=
(
65
−
t
)
(
200
+
5
t
)
−
45
t
.
.
.
.
.
.
(
1
)
P=(65-t)(200+5t)-45t…… (1)
P
=
(
65
−
t
)
(
200
+
5
t
)
−
45
t
……
(
1
)
容易得出当
t
=
8
t=8
t
=
8
时,P取最大值
13320
13320
13320
元。
其实,大多数情况下,问题到这里就已划上句号。但现实生活中,稍微细心一点,我们会发现在上述模型的参数中,牛的重量,当前市场价格、每天饲料钱3个参数都是很容易测量的,即确定性较大,但牛的生长率和市场价格的下降率2个参数则不是那么好确定,例子中虽然规定了市场价格下降率r=1元/天,但实际中,每天的r都是不一样的。
于是我们会有一个疑惑——
是不是对于所有的市场价格下降率,这个模型都适用?
为了消除疑惑,我们分别随便选取原下降率(1元/天)周围的几个数 r=0.8, 0.9, 1.0, 1.1, 1.2,根据公式(1),分别得出t=15, 11, 8, 5, 3 ,得下图:

三、如何进行
灵敏度分析,就是将市场价格下降率
r
r
r
作为未知参数,计算最佳卖出时间t和r关系,将每天下降1元 改为每天下降r元
模型改变为

于是得到了灵敏度关系——r-t关系,绘制图像如下
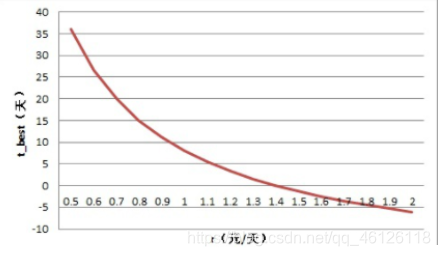
公式(2)和上图的意义在于——作为牛贩子,我能确定一个r-t关系,确保我在不同r下,都能确定最佳卖牛时间 t。当0<r<2.8时,最佳卖出时间就由公式(2)给出;当 r>2.8 时, t<0 ,这会导致P(t)是一个始终下降的曲线,这意味着,最佳卖牛时间为 t=0 ,也就是说,一旦市场价格下降率 r>2.8,需要当天就把牛卖掉,这时候饲养牛已经没有任何经济价值了
然而,在实际使用中,我们更多地是将这种灵敏性关系表示成相对改变量或百分比改变的形式。例如, r 的10%的下降,导致了 t 的38%的增加。


四、灵敏度分析用处

五、什么时候进行
灵敏性分析的成功应用通常要有较好的判断力,通常既不可能对模型中的每个参数都计算灵敏性系数,也没有这种特别的要求。我们需要选择那些有较大不确定性的参数进行灵敏性分析。对灵敏性系数的解释还要依赖于参数的不确定程度。原始问题中数据的不确定程度会影响我们对答案的自信度。在这个售猪问题中,我们通常认为猪的生长率g 比价格的下降率r更可靠.如果我们观察了猪或其他类似动物在过去的生长情况,g有25%的误差会是很不寻常的,但对r的估计有25%的误差则不足为奇。
因此,灵敏度分析也是为了让自己所建的模型更具备一定的说服力。如果你建立的模型中核心参数仅仅对在某个点处可以比较好的解决问题,取其它值时,就不起作用了。那么这个模型的普适性就不强。