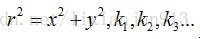摄像机标定——标定原理
一:摄像机成像原理

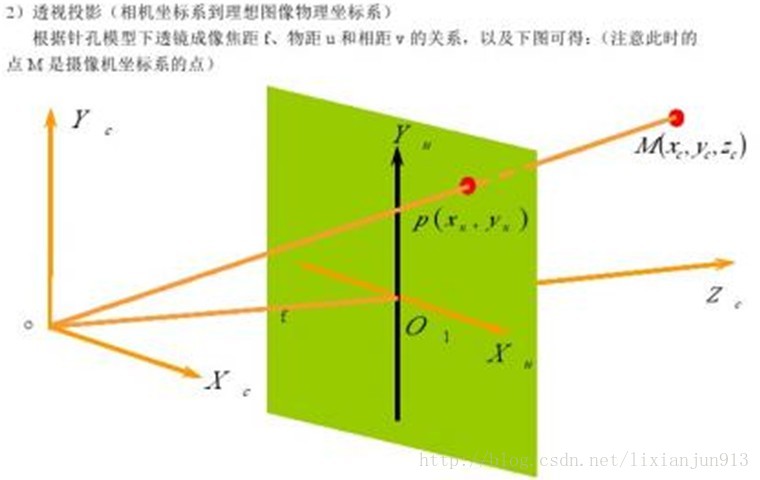
摄像机成像模型一般有三种:透镜投影模型(小孔摄像机模型)、正交投影模型和透视投影模型
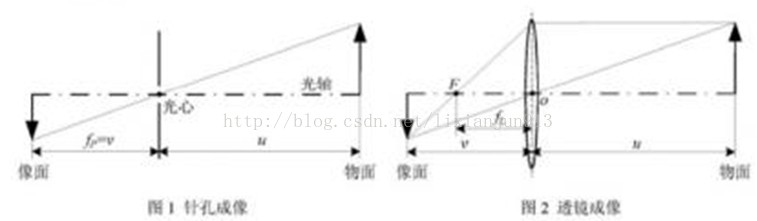
光学中最基本的高斯成像公式:1/u + 1/v = 1/f (式一)
原理图如下:
二:认识三个坐标系
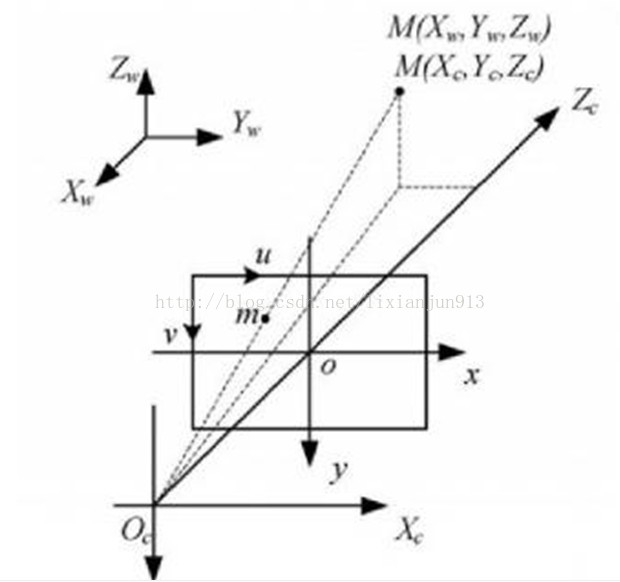
三个坐标系的关系图
如上图表示的三个坐标系分别为世界坐标系,摄像机坐标系,图像坐标系
1:世界坐标系(Xw Yw Zw)
用户定义的空间三维坐标系,用来描述三维空间中的物体和相机之间的坐标位置,满足右手法则
2:摄像机坐标系(Xc Yc Zc)
以相机的光心作为原点,Zc轴与光轴重合,并垂直于成像平面,且取摄影方向为正方向,Xc、Yc轴与图像物理坐标系的x,y轴平行,且OcO为摄像机的焦距f
3:图像坐标系
是以图像的左上方为原点,的图像坐标系(u v)(此坐标以像素为单位),这里我们建立了图像物理坐标系(x y)为xoy坐标系(此坐标系以毫米为单位)。
三:相机标定原理
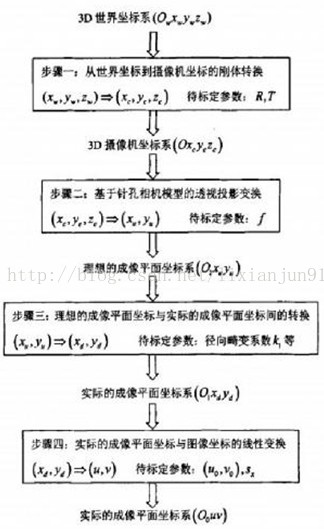
1:刚体变换
刚体变换的过程就是世界坐标系中的一点到摄像机坐标系中的点,可以由一个旋转矩阵R和一个平移矩阵t来描述,则存在如下刚体变换公式:

3:几何畸变
由于摄像机制造工艺偏差,以及入射光线在通过各个透镜时的折射误差和CCD点阵位置误差等,实际的光学系统存在着非线性几何失真,从而使目标像点与理论像点之间存在着多种几何畸变。

几何畸变主要包括径向畸变、切向畸变和薄棱镜畸变。
1) 径向畸变
径向畸变可分为枕形畸变和桶形畸变,主要由镜头形状缺陷造成。径向畸变效果图如图
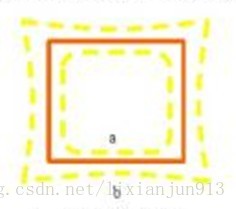
其数学模型为:

其中,
为径向畸变系数。
2) 切向畸变
切向畸变主要包括离心畸变和薄棱镜畸变。其中,离心畸变是由摄像机的镜头中各透镜的光轴不能完全重合造成的。
切向畸变的数学模型可表示为:
综上可得理想图像点坐标和实际图像点坐标之间的关系可表示为:
其中,
是理想图像点的坐标。
3) 薄棱镜畸变
薄棱镜畸变是由镜头设计和制造缺陷等误差造成的,比如镜头与摄像机像面之间有很小的倾角等。这类畸变就相当于是在光学系统中附加了一个薄棱镜,所以它不仅会引起径向偏差,而且还会引起切向误差。薄棱镜畸变的数学模型为:
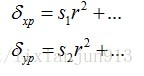


针孔相机模型和变形
针孔摄像机模型,就是一幅视图是通过透视变换将三维空间中的点投影到图像平面。投影公式如下:
![s \cdot m' = A\cdot[R|t] \cdot M'](http://wiki.opencv.org.cn/images/math/829b582e8196dc7c221c301a1c02fbc6.png)
或者

(yjf:注意这里的矩阵R为旋转矩阵,即只由绕3个轴的旋转矩阵组合得到的矩阵,它的9个元素并不独立,事实上它只有需三个参数就可以描述了)
这里(X, Y, Z)是一个点的世界坐标,(u, v)是点投影在图像平面的坐标,以像素为单位。A被称作摄像机矩阵,或者内参数矩阵。(cx, cy)是基准点(通常在图像的中心)【yjf:应该这样表述:是图像面与相机光轴的交点处像素的坐标,通常这个点是图像中点】,fx, fy是以像素为单位的焦距【yjf:fx=f/Sx,fy=f/Sy其中f为焦距,Sx,Sy分别为一个像素CCD单元的x,y方向的实际长度】。所以如果因为某些因素对来自于摄像机的一幅图像升采样或者降采样,所有这些参数(fx, fy, cx和cy)都将被缩放(乘或者除)同样的尺度。内参数矩阵不依赖场景的视图,一旦计算出,可以被重复使用(只要焦距固定)。旋转-平移矩阵[R|t]被称作外参数矩阵,它用来描述相机相对于一个固定场景的运动,或者相反,物体围绕相机的的刚性运动【yjf:[R|t]的作用是得到物体在 xy平面与成像面平行z轴和相机光轴相共线的一个三维坐标系(可称为摄像机坐标系) 下的坐标表示】。也就是[R|t]将点(X, Y, Z)的坐标变换到某个坐标系,这个坐标系相对于摄像机来说是固定不变的。上面的变换等价与下面的形式(z≠0):

x
‘ =
x
/
z
y
‘ =
y
/
z


真正的镜头通常有一些形变,主要的变形为径向形变,也会有轻微的切向形变。所以上面的模型可以扩展为:

x
‘ =
x
/
z
y
‘ =
y
/
z


这里
r
2 =
x
‘2 +
y
‘2


k
1和
k
2是径向形变系数,
p
1和
p
1是切向形变系数。OpenCV中没有考虑高阶系数。形变系数跟拍摄的场景无关,因此它们是内参数,而且与拍摄图像的分辨率无关。
后面的函数使用上面提到的模型来做如下事情:
- 给定内参数和外参数,投影三维点到图像平面。
- 给定内参数、几个三维点坐标和其对应的图像坐标,来计算外参数。
- 根据已知的定标模式,从几个角度(每个角度都有几个对应好的3D-2D点对)的照片来计算相机的外参数和内参数。