很多人都听说过贝叶斯原理,在哪听说过?基本上是在学概率统计的时候知道的。有些人可能会说,我记不住这些概率论的公式,没关系,我尽量用通俗易懂的语言进行讲解。
贝叶斯原理是英国数学家托马斯·贝叶斯提出的。贝叶斯是个很神奇的人,他的经历类似梵高。生前没有得到重视,死后,他写的一篇关于归纳推理的论文被朋友翻了出来,并发表了。这一发表不要紧,结果这篇论文的思想直接影响了接下来两个多世纪的统计学,是科学史上著名的论文之一。
贝叶斯原理跟我们的生活联系非常紧密。举个例子,如果你看到一个人总是花钱,那么会推断这个人多半是个有钱人。当然这也不是绝对,也就是说,当你不能准确预知一个事物本质的时候,你可以依靠和事物本质相关的事件来进行判断,如果事情发生的频次多,则证明这个属性更有可能存在。
贝叶斯原理
贝叶斯原理是怎么来的呢?贝叶斯为了解决一个叫“逆向概率”问题写了一篇文章,尝试解答在没有太多可靠证据的情况下,怎样做出更符合数学逻辑的推测。
什么是“逆向概率”呢?
所谓“逆向概率”是相对“正向概率”而言。正向概率的问题很容易理解,比如我们已经知道袋子里面有 N 个球,不是黑球就是白球,其中 M 个是黑球,那么把手伸进去摸一个球,就能知道摸出黑球的概率是多少。但这种情况往往是上帝视角,即了解了事情的全貌再做判断。
在现实生活中,我们很难知道事情的全貌。贝叶斯则从实际场景出发,提了一个问题:如果我们事先不知道袋子里面黑球和白球的比例,而是通过我们摸出来的球的颜色,能判断出袋子里面黑白球的比例么?
正是这样的一个问题,影响了接下来近 200 年的统计学理论。这是因为,贝叶斯原理与其他统计学推断方法截然不同,它是建立在主观判断的基础上:在我们不了解所有客观事实的情况下,同样可以先估计一个值,然后根据实际结果不断进行修正。
我们用一个题目来体会下:假设有一种病叫做“贝叶死”,它的发病率是万分之一,即 10000 人中会有 1 个人得病。现有一种测试可以检验一个人是否得病的准确率是 99.9%,它的误报率是 0.1%,那么现在的问题是,如果一个人被查出来患有“叶贝死”,实际上患有的可能性有多大?
你可能会想说,既然查出患有“贝叶死”的准确率是 99.9%,那是不是实际上患“贝叶死”的概率也是 99.9% 呢?实际上不是的。你自己想想,在 10000 个人中,还存在 0.1% 的误查的情况,也就是 10 个人没有患病但是被诊断成阳性。当然 10000 个人中,也确实存在一个患有贝叶死的人,他有 99.9% 的概率被检查出来。所以你可以粗算下,患病的这个人实际上是这 11 个人里面的一员,即实际患病比例是 1/11≈9%。
上面这个例子中,实际上涉及到了贝叶斯原理中的几个概念:
先验概率:
通过经验来判断事情发生的概率,比如说“贝叶死”的发病率是万分之一,就是先验概率。再比如南方的梅雨季是 6-7 月,就是通过往年的气候总结出来的经验,这个时候下雨的概率就比其他时间高出很多。
后验概率:
后验概率就是发生结果之后,推测原因的概率。比如说某人查出来了患有“贝叶死”,那么患病的原因可能是 A、B 或 C。患有“贝叶死”是因为原因 A 的概率就是后验概率。它是属于条件概率的一种。
条件概率:
事件 A 在另外一个事件 B 已经发生条件下的发生概率,表示为 P(A|B),读作“在 B 发生的条件下 A 发生的概率”。比如原因 A 的条件下,患有“贝叶死”的概率,就是条件概率。
似然函数(likelihood function):
你可以把概率模型的训练过程理解为求参数估计的过程。举个例子,如果一个硬币在 10 次抛落中正面均朝上。那么你肯定在想,这个硬币是均匀的可能性是多少?这里硬币均匀就是个参数,似然函数就是用来衡量这个模型的参数。似然在这里就是可能性的意思,它是关于统计参数的函数。
介绍完贝叶斯原理中的这几个概念,我们再来看下贝叶斯原理,实际上贝叶斯原理就是求解后验概率,我们假设:A 表示事件 “测出为阳性”, 用 B1 表示“患有贝叶死”, B2 表示“没有患贝叶死”。根据上面那道题,我们可以得到下面的信息。
患有贝叶死的情况下,测出为阳性的概率为 P(A|B1)=99.9%,没有患贝叶死,但测出为阳性的概率为 P(A|B2)=0.1%。另外患有贝叶死的概率为 P(B1)=0.01%,没有患贝叶死的概率 P(B2)=99.99%。
那么我们检测出来为阳性,而且是贝叶死的概率 P(B1,A)=P(B1)*P(A|B1)=0.01%*99.9%=0.00999%。
这里 P(B1,A) 代表的是联合概率,同样我们可以求得 P(B2,A)=P(B2)*P(A|B2)=99.99%*0.1%=0.09999%。
然后我们想求得是检查为阳性的情况下,患有贝叶死的概率,也即是 P(B1|A)。
所以检查出阳性,且患有贝叶死的概率为:
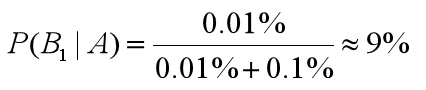
检查出是阳性,但没有患有贝叶死的概率为:
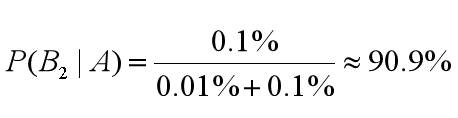
这里我们能看出来 0.01%+0.1% 均出现在了 P(B1|A) 和 P(B2|A) 的计算中作为分母。我们把它称之为论据因子,也相当于一个权值因子。
其中 P(B1)、P(B2) 就是先验概率,我们现在知道了观测值,就是被检测出来是阳性,来求患贝叶死的概率,也就是求后验概率。求后验概率就是贝叶斯原理要求的,基于刚才求得的 P(B1|A),P(B2|A),我们可以总结出贝叶斯公式为:
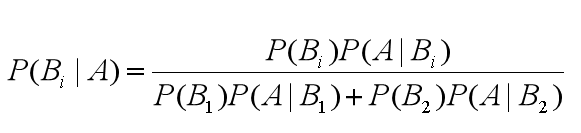
由此,我们可以得出通用的贝叶斯公式:
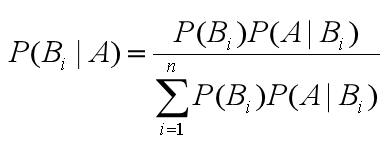
朴素贝叶斯
讲完贝叶斯原理之后,我们再来看下今天重点要讲的算法,朴素贝叶斯。它是一种简单但极为强大的预测建模算法。之所以称为朴素贝叶斯,是因为它假设每个输入变量是独立的。这是一个强硬的假设,实际情况并不一定,但是这项技术对于绝大部分的复杂问题仍然非常有效。
朴素贝叶斯模型由两种类型的概率组成:
1.每个类别的概率P(Cj);
2.每个属性的条件概率P(Ai|Cj)。
我来举个例子说明下什么是类别概率和条件概率。假设我有 7 个棋子,其中 3 个是白色的,4 个是黑色的。那么棋子是白色的概率就是 3/7,黑色的概率就是 4/7,这个就是类别概率。
假设我把这 7 个棋子放到了两个盒子里,其中盒子 A 里面有 2 个白棋,2 个黑棋;盒子 B 里面有 1 个白棋,2 个黑棋。那么在盒子 A 中抓到白棋的概率就是 1/2,抓到黑棋的概率也是 1/2,这个就是条件概率,也就是在某个条件(比如在盒子 A 中)下的概率。
在朴素贝叶斯中,我们要统计的是属性的条件概率,也就是假设取出来的是白色的棋子,那么它属于盒子 A 的概率是 2/3。
为了训练朴素贝叶斯模型,我们需要先给出训练数据,以及这些数据对应的分类。那么上面这两个概率,也就是类别概率和条件概率。他们都可以从给出的训练数据中计算出来。一旦计算出来,概率模型就可以使用贝叶斯原理对新数据进行预测。

另外我想告诉你的是,贝叶斯原理、贝叶斯分类和朴素贝叶斯这三者之间是有区别的。
贝叶斯原理是最大的概念,它解决了概率论中“逆向概率”的问题,在这个理论基础上,人们设计出了贝叶斯分类器,朴素贝叶斯分类是贝叶斯分类器中的一种,也是最简单,最常用的分类器。朴素贝叶斯之所以朴素是因为它假设属性是相互独立的,因此对实际情况有所约束,如果属性之间存在关联,分类准确率会降低。不过好在对于大部分情况下,朴素贝叶斯的分类效果都不错。

朴素贝叶斯分类工作原理
朴素贝叶斯分类是常用的贝叶斯分类方法。我们日常生活中看到一个陌生人,要做的第一件事情就是判断 TA 的性别,判断性别的过程就是一个分类的过程。根据以往的经验,我们通常会从身高、体重、鞋码、头发长短、服饰、声音等角度进行判断。这里的“经验”就是一个训练好的关于性别判断的模型,其训练数据是日常中遇到的各式各样的人,以及这些人实际的性别数据。
离散数据案例
我们遇到的数据可以分为两种,一种是离散数据,另一种是连续数据。那什么是离散数据呢?离散就是不连续的意思,有明确的边界,比如整数 1,2,3 就是离散数据,而 1 到 3 之间的任何数,就是连续数据,它可以取在这个区间里的任何数值。
我以下面的数据为例,这些是根据你之前的经验所获得的数据。然后给你一个新的数据:身高“高”、体重“中”,鞋码“中”,请问这个人是男还是女?
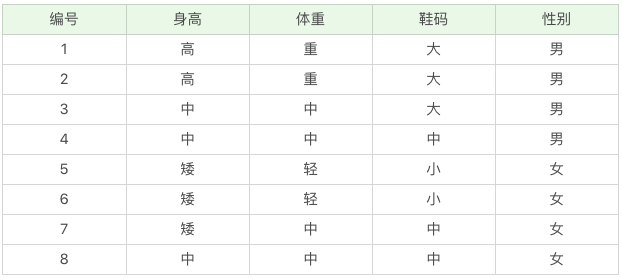
针对这个问题,我们先确定一共有 3 个属性,假设我们用 A 代表属性,用 A1, A2, A3 分别为身高 = 高、体重 = 中、鞋码 = 中。一共有两个类别,假设用 C 代表类别,那么 C1,C2 分别是:男、女,在未知的情况下我们用 Cj 表示。
那么我们想求在 A1、A2、A3 属性下,Cj 的概率,用条件概率表示就是 P(Cj|A1A2A3)。根据上面讲的贝叶斯的公式,我们可以得出:
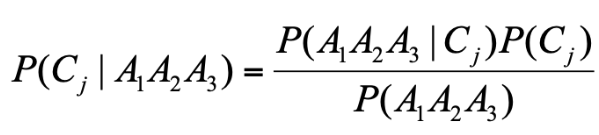
因为一共有 2 个类别,所以我们只需要求得 P(C1|A1A2A3) 和 P(C2|A1A2A3) 的概率即可,然后比较下哪个分类的可能性大,就是哪个分类结果。
在这个公式里,因为 P(A1A2A3) 都是固定的,我们想要寻找使得 P(Cj|A1A2A3) 的最大值,就等价于求 P(A1A2A3|Cj)P(Cj) 最大值。
我们假定 Ai 之间是相互独立的,那么:
P(A1A2A3|Cj)=P(A1|Cj)P(A2|Cj)P(A3|Cj)
然后我们需要从 Ai 和 Cj 中计算出 P(Ai|Cj) 的概率,带入到上面的公式得出 P(A1A2A3|Cj),最后找到使得 P(A1A2A3|Cj) 最大的类别 Cj。
我分别求下这些条件下的概率:
P(A1|C1)=1/2, P(A2|C1)=1/2, P(A3|C1)=1/4,P(A1|C2)=0, P(A2|C2)=1/2, P(A3|C2)=1/2,所以 P(A1A2A3|C1)=1/16, P(A1A2A3|C2)=0。
因为 P(A1A2A3|C1)P(C1)>P(A1A2A3|C2)P(C2),所以应该是 C1 类别,即男性。
连续数据案例
我们做了一个离散的数据案例,实际生活中我们得到的是连续的数值,比如下面这组数据:
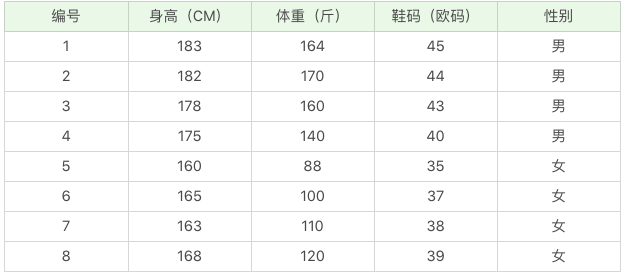
那么如果给你一个新的数据,身高 180、体重 120,鞋码 41,请问该人是男是女呢?
公式还是上面的公式,这里的困难在于,由于身高、体重、鞋码都是连续变量,不能采用离散变量的方法计算概率。而且由于样本太少,所以也无法分成区间计算。怎么办呢?
这时,可以假设男性和女性的身高、体重、鞋码都是正态分布,通过样本计算出均值和方差,也就是得到正态分布的密度函数。有了密度函数,就可以把值代入,算出某一点的密度函数的值。比如,男性的身高是均值 179.5、标准差为 3.697 的正态分布。所以男性的身高为 180 的概率为 0.1069。怎么计算得出的呢? 你可以使用 EXCEL 的 NORMDIST(x,mean,standard_dev,cumulative) 函数,一共有 4 个参数:
1.x:正态分布中,需要计算的数值;
2.Mean:正态分布的平均值;
3.Standard_dev:正态分布的标准差;
4.Cumulative:取值为逻辑值,即 False 或 True。它决定了函数的形式。当为 TRUE 时,函数结果为累积分布;为 False 时,函数结果为概率密度。
这里我们使用的是 NORMDIST(180,179.5,3.697,0)=0.1069。
同理我们可以计算得出男性体重为 120 的概率为 0.000382324,男性鞋码为 41 号的概率为 0.120304111。
所以我们可以计算得出:
P(A1A2A3|C1)=P(A1|C1)P(A2|C1)P(A3|C1)=0.10690.0003823240.120304111=4.9169e-6
同理我们也可以计算出来该人为女的可能性:
P(A1A2A3|C2)=P(A1|C2)P(A2|C2)P(A3|C2)=0.000001474890.0153541440.120306074=2.7244e-9
很明显这组数据分类为男的概率大于分类为女的概率。
当然在 Python 中,有第三方库可以直接帮我们进行上面的操作,这个我们会在下节课中介绍。这里主要是给你讲解下具体的运算原理。
朴素贝叶斯分类器工作流程
朴素贝叶斯分类常用于文本分类,尤其是对于英文等语言来说,分类效果很好。它常用于垃圾文本过滤、情感预测、推荐系统等。
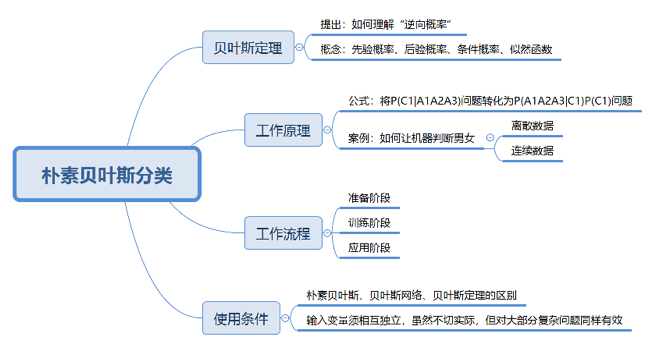
流程可以用下图表示:

从图片你也可以看出来,朴素贝叶斯分类器需要三个流程,我来给你一一讲解下这几个流程。
第一阶段:准备阶段
在这个阶段我们需要确定特征属性,比如上面案例中的“身高”、“体重”、“鞋码”等,并对每个特征属性进行适当划分,然后由人工对一部分数据进行分类,形成训练样本。
这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段,其质量对整个过程将有重要影响,分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。
第二阶段:训练阶段
这个阶段就是生成分类器,主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率。
输入是特征属性和训练样本,输出是分类器。
第三阶段:应用阶段
这个阶段是使用分类器对新数据进行分类。输入是分类器和新数据,输出是新数据的分类结果。
好了,在这次课中你了解了概率论中的贝叶斯原理,朴素贝叶斯的工作原理和工作流程,也对朴素贝叶斯的强大和限制有了认识。下一节中,我将带你实战,亲自掌握 Python 中关于朴素贝叶斯分类器工具的使用。
最后给你留两道思考题吧,第一道题,离散型变量和连续变量在朴素贝叶斯模型中的处理有什么差别呢?
第二个问题是,如果你的女朋友,在你的手机里发现了和别的女人的暧昧短信,于是她开始思考了 3 个概率问题,你来判断下下面的 3 个概率分别属于哪种概率:
你在没有任何情况下,出轨的概率;
如果你出轨了,那么你的手机里有暧昧短信的概率;
在你的手机里发现了暧昧短信,认为你出轨的概率。这三种概率分别属于先验概率、后验概率和条件概率的哪一种?