训练简单的机器学习分类算法
一、人工神经元
1.人工神经元定义
可以将人工神经元逻辑放在二元分类场景,将两个类分别命名为1(正类)和-1(负类),定义决策函数(φ(z)),接受输入值x及其相应权重w,z为输入值与权重的乘积累加和,z=W1X1+…+WmXm:
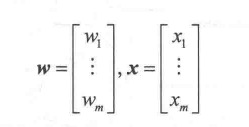
如果某个特定样本的净输入值x(i)比定义的阈值θ大,则预测结果为1,否则为-1
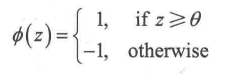
为了简化,把阈值θ放到等式左边,权重零定义为w0=-θ,x0=1,这样z为
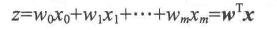
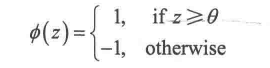
机器学习中通常称w0=-θ称为偏置。
2.感知器学习规则
感知器规则可以总结为以下几部:
1.把权重初始化为0或者小的随机数
2.对每个训练样本:*计算输出值 *更新权重
输出值为单位阶跃函数预测的预先定义好的类标签,同时更新权重向量w的每个值wj,表达式为:
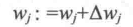
Δwj是用来更新wj的值,该值根据感知器的学习规则计算:
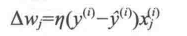
η为学习率,一般是一个0.0到1.0之间的常数,yi为第i个训练样本的正确类标签,后面的yi为预测的类标签,并且所有权重更新之前,不会重新计算预测的类标签,二维数据集的更新可以表示为:
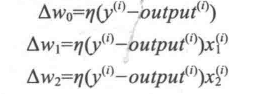
在感知机正确预测分类标签的两种情况下,权重保持不变:
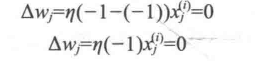
但是如果预测出错,权重会偏向正或负的目标类
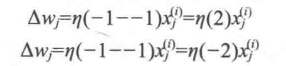
二、在python中实现感知器学习算法
1.面向对象的感知器API
可以用面向对象的方法把感知机接口定义为一个python类,它允许初始化新的perceptron对象,这些对象可以通过fit方法从数据中学习,并通过单独的predict方法进行预测,作为约定,我们在对象初始化时未创建但通过对象的其他方法创建的属性的后面添加下划线,例如self.w_
fit方法实现的功能简单来说就是求训练集X的均值,方差,最大值,最小值等固有属性,可以理解为一个训练过程
下面代码实现了感知器:
class Perceptron(object):
"""Perceptron classifier.
Parameters
------------
eta : float
Learning rate (between 0.0 and 1.0)
n_iter : int
Passes over the training dataset.
random_state : int
Random number generator seed for random weight
initialization.
Attributes
-----------
w_ : 1d-array
Weights after fitting.
errors_ : list
Number of misclassifications (updates) in each epoch.
"""
def __init__(self, eta=0.01, n_iter=50, random_state=1):
self.eta = eta
self.n_iter = n_iter
self.random_state = random_state
def fit(self, X, y):
"""Fit training data.
Parameters
----------
X : {array-like}, shape = [n_samples, n_features]
Training vectors, where n_samples is the number of samples and
n_features is the number of features.
y : array-like, shape = [n_samples]
Target values.
Returns
-------
self : object
"""
rgen = np.random.RandomState(self.random_state)
self.w_ = rgen.normal(loc=0.0, scale=0.01, size=1 + X.shape[1])
self.errors_ = []
for _ in range(self.n_iter):
errors = 0
for xi, target in zip(X, y):
update = self.eta * (target - self.predict(xi))
self.w_[1:] += update * xi
self.w_[0] += update
errors += int(update != 0.0)
self.errors_.append(errors)
return self
def net_input(self, X):
"""Calculate net input"""
return np.dot(X, self.w_[1:]) + self.w_[0]
def predict(self, X):
"""Return class label after unit step"""
return np.where(self.net_input(X) >= 0.0, 1, -1)
这段实现感知器的代码用所给的学习率eta和迭代次数n_iter初始化新的perceptron对象,通过fit方法,初始化self.w_的权重,并把数据存入向量代表数据集的维数或特征数。
该向量包含来源于正态分布的小随机数,通过调用rgen.normal产生标准差为0.01的正态分布,其中rgen为随机数生成器。
初始化权重后,用fit方法遍历训练集的所有样本,并根据规则更新权重,fit方法调用predict方法来预测分类标签并更新权重。另外将分类错误记录在self.errors列表中。用net_input方法中的np.dot函数来计算向量点积w的转置x
注:numpy中dot()函数主要功能有两个:向量点积和矩阵乘法
格式:x.dot(y)等价于np.dot(x,y),其中x是m*n的矩阵,y是n*m的矩阵,x.dot(y)得到m*m矩阵
2.在鸢尾花数据集上训练感知器模型
在此例子中,我们将从鸢尾花数据集加载setosa和versicolor两种花的数据,实际上感知器并不限于两个维度,感知器算法可以扩展带多元分类,例如一对全部(OvA)的技术。
OvA技术也称为一对其余(OvR),可以把分类器从二元扩展到多元的一种技术,OvA可以为每个类训练一个分类器,所训练的类被视为正类,所有其他类的样本都被视为负类,在目标检测相关项目上,对于一张图片上的样本,有分类的视为正样本,背景则被视为负样本,与感知器相似。
对于鸢尾花数据集的分类,我们可以利用pandas库,从UCI机器学习库把鸢尾花数据集直接加载到DataFrame对象,然后用tail方法把把最后5行数据列出来以确保数据加载的正确性。
import pandas as pd
df =pd.read_csv(iris.data,header=None)
df.tail()



接下来提取与50朵iris-setosa和50朵iris-versicolor鸢尾花相对应的前100个类标签,然后转换为整数型的类标签1(versicolor)和-1(setosa),并存入向量y,再调用pandas的DataFrame的方法获得到相应的Numpy表示。
同样可以从100个训练样本中提取特征的第一列(萼片长度)和第三列(花瓣长度),并将它们存入特征矩阵X,然后经过可视化处理形成二维散点图
import matplotlib.pyplot as plt
y=df.iloc[0:100,4].values
y = np.where(y == 'Iris-setosa', -1, 1)
X = df.iloc[0:100, [0, 2]].values
plt.scatter(X[:50, 0], X[:50, 1],
color='red', marker='o', label='setosa')
plt.scatter(X[50:100, 0], X[50:100, 1],
color='blue', marker='x', label='versicolor')
plt.xlabel('sepal length [cm]')
plt.ylabel('petal length [cm]')
plt.legend(loc='upper left')
plt.show()
执行代码后产生二维散点图

散点图显示了莺尾花数据集的样本在花瓣长度和萼片长度两个特征轴的分布情况,一个线性的决策边界足以把setosa花与versicolor花区别开,因此,感知器这样的线性分类器能够完美对数据集中的花朵进行分类。
然后我们需要在鸢尾花数据子集上训练感知器算法,另外将绘制每个迭代的分类错误,以检查算法是否收敛,并找到分隔两类鸢尾花的决策边界
ppn = Perceptron(eta=0.1, n_iter=10)
ppn.fit(X, y)
plt.plot(range(1, len(ppn.errors_) + 1), ppn.errors_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Number of updates')
plt.show()
执行前面的代码,可以看到分类错误与迭代之间的关系

感知器在第6次迭代后开始收敛,现在应该能够完美地对训练样本进行分类,下面进行二维数据决策边界可视化
def plot_decision_regions(X, y, classifier, resolution=0.02):
# setup marker generator and color map
markers = ('s', 'x', 'o', '^', 'v')
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(y))])
# plot the decision surface
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
plt.contourf(xx1, xx2, Z, alpha=0.3, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
# plot class samples
for idx, cl in enumerate(np.unique(y)):
plt.scatter(x=X[y == cl, 0],
y=X[y == cl, 1],
alpha=0.8,
c=colors[idx],
marker=markers[idx],
label=cl,
edgecolor='black')
首先定义颜色和标记并通过ListedColormap来从颜色列表创建色度图,然后通过Numpy的meshgrid函数创建网格阵列xx1和xx2,利用特征向量确定特征的最小和最大值,由于在两个特征维度上训练感知器分类器,这样就可以调用predict方法来预测相应网格点的分类标签z
把预测获得的分类标签z改造成与xx1和xx2相同维数的网格后,现在可以通过调用Matplotlib的contourf函数画出轮廓图,并且把网格阵列中每个预测的分类结果标注在不同颜色的决策区域。
plot_decision_regions(X, y, classifier=ppn)
plt.xlabel('sepal length [cm]')
plt.ylabel('petal length [cm]')
plt.legend(loc='upper left')
plt.show()
执行后结果如图

这样就通过学习掌握了决策边界,能够把鸢尾花训练集的样本完美分开
三、自适应神经元和学习收敛
自适应感知器(Adaline)是感知器的优化和改进,Adaline规则和感知器之间的关键差异在于Adaline规则的权重更新时基于线性激活函数,而感知器是基于单位阶跃函数,Adaline的线性激活函数φ(z)是净输入的等同函数
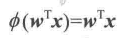
虽然线性激活函数可用于学习权重,但仍然使用阈值函数做最终预测,这类似与先前的单位阶跃函数,下图是感知器与自适应算法的主要区别:

1.梯度下降为最小代价函数
有监督机器学习算法的一个关键是在学习过程中优化目标函数,该目标函数通常是要最小化的代价函数,对自适应神经元而言,可以把学习权重的代价函数J定义为在计算结果和真正的分类标签之间的误差平方和
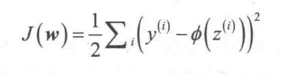
2.用python实现Adaline
class AdalineGD(object):
"""ADAptive LInear NEuron classifier.
Parameters
------------
eta : float
Learning rate (between 0.0 and 1.0)
n_iter : int
Passes over the training dataset.
random_state : int
Random number generator seed for random weight
initialization.
Attributes
-----------
w_ : 1d-array
Weights after fitting.
cost_ : list
Sum-of-squares cost function value in each epoch.
"""
def __init__(self, eta=0.01, n_iter=50, random_state=1):
self.eta = eta
self.n_iter = n_iter
self.random_state = random_state
def fit(self, X, y):
""" Fit training data.
Parameters
----------
X : {array-like}, shape = [n_samples, n_features]
Training vectors, where n_samples is the number of samples and
n_features is the number of features.
y : array-like, shape = [n_samples]
Target values.
Returns
-------
self : object
"""
rgen = np.random.RandomState(self.random_state)
self.w_ = rgen.normal(loc=0.0, scale=0.01, size=1 + X.shape[1])
self.cost_ = []
for i in range(self.n_iter):
net_input = self.net_input(X)
# Please note that the "activation" method has no effect
# in the code since it is simply an identity function. We
# could write `output = self.net_input(X)` directly instead.
# The purpose of the activation is more conceptual, i.e.,
# in the case of logistic regression (as we will see later),
# we could change it to
# a sigmoid function to implement a logistic regression classifier.
output = self.activation(net_input)
errors = (y - output)
self.w_[1:] += self.eta * X.T.dot(errors)
self.w_[0] += self.eta * errors.sum()
cost = (errors**2).sum() / 2.0
self.cost_.append(cost)
return self
def net_input(self, X):
"""Calculate net input"""
return np.dot(X, self.w_[1:]) + self.w_[0]
def activation(self, X):
"""Compute linear activation"""
return X
def predict(self, X):
"""Return class label after unit step"""
return np.where(self.activation(self.net_input(X)) >= 0.0, 1, -1)