解决的问题
我们提出了一个稳定的方法来半监督地学习图结构的数据,这种方法基于一种卷积网络的变体,是将卷积网络直接作用在图上。我们是基于对一种谱图卷积的一阶近似选择的这种卷积结构。我们的模型能够学到既可以编码局部的图结构也可以编码结点特征的隐藏层表示。在引文网络和知识图谱数据集上进行的一系列实验表明,我们的方法跟类似方法相比有显著的提升。
问题形式化
本文考虑的是对图上的结点进行分类,而图中只有一小部分结点有标签。这类问题可以被形式化为基于图的半监督学习,其中标签信息通过一些显式的基于图的正则来进行平滑,例如在loss函数中加上拉普拉斯正则。
L
=
L
0
+
λ
L
r
e
g
L = L_0 + \lambda L_{reg}
L
=
L
0
+
λ
L
r
e
g
L
r
e
g
=
∑
i
,
j
A
i
j
∣
∣
f
(
X
i
)
−
f
(
X
j
)
∣
∣
2
=
f
(
X
)
T
Δ
f
(
X
)
L_{reg} = \sum_{i, j}A_{ij}||f(X_i) – f(X_j)||^2 = f(X)^T \Delta f(X)
L
r
e
g
=
i
,
j
∑
A
i
j
∣
∣
f
(
X
i
)
−
f
(
X
j
)
∣
∣
2
=
f
(
X
)
T
Δ
f
(
X
)
这里
L
0
L_0
L
0
代表监督学习的loss,
f
(
⋅
)
f(\cdot)
f
(
⋅
)
可以是一个神经网络类的函数,
λ
\lambda
λ
是一个权重参数,
X
X
X
是结点特征向量
X
i
X_i
X
i
的矩阵。
Δ
=
D
−
A
\Delta = D – A
Δ
=
D
−
A
是未正则化的无向图
G
=
(
V
,
ϵ
)
G=(V, \epsilon)
G
=
(
V
,
ϵ
)
的图拉普拉斯矩阵。其中
v
i
∈
V
v_i \in V
v
i
∈
V
表示图的结点,而
(
v
i
,
v
j
)
∈
ϵ
(v_i, v_j) \in \epsilon
(
v
i
,
v
j
)
∈
ϵ
表示图的边,
A
∈
R
N
×
N
A \in R^{N \times N}
A
∈
R
N
×
N
是图的临界矩阵,
D
i
i
=
∑
j
A
i
j
D_{ii} = \sum_j A_{ij}
D
i
i
=
∑
j
A
i
j
是一个度的矩阵。上式基于的假设是相邻结点很可能有相同的label。然而这种假设可能会限制模型的表现,因为图的边可能并不是只表征相似性,很有可能包含其他信息。
本文中我们直接利用神经网络模型
f
(
X
,
A
)
f(X, A)
f
(
X
,
A
)
为图结构编码,并且为全部有label的结点进行监督学习训练。利用临界矩阵来得到
f
(
⋅
)
f(\cdot)
f
(
⋅
)
使得模型用监督学习的loss
L
0
L_0
L
0
来计算梯度,这个梯度既可以用来学习有标签结点也可以用来学习无标签结点的表示。
下面来介绍本文中基于图的神经网络模型
f
(
X
,
A
)
f(X, A)
f
(
X
,
A
)
的理论基础。我们考虑一个有如下layer-wise传播规则的多层图卷积:
H
(
l
+
1
)
=
σ
(
D
~
−
1
2
A
~
D
~
−
1
2
H
(
l
)
W
(
l
)
)
H^{(l+1)} = \sigma (\widetilde{D}^{-\frac{1}{2}}\widetilde{A}\widetilde{D}^{-\frac{1}{2}}H^{(l)}W^{(l)})
H
(
l
+
1
)
=
σ
(
D
−
2
1
A
D
−
2
1
H
(
l
)
W
(
l
)
)
这里
A
~
=
A
+
I
N
\widetilde{A} = A + I_N
A
=
A
+
I
N
是加上了self-connection的无向图的邻接矩阵,
I
N
I_N
I
N
是单位矩阵,
D
~
i
i
=
∑
j
A
~
i
j
\widetilde{D}_{ii} = \sum_j \widetilde{A}_{ij}
D
i
i
=
∑
j
A
i
j
,
W
(
l
)
W^{(l)}
W
(
l
)
是一个layer-specific的权重矩阵,
σ
(
⋅
)
\sigma(\cdot)
σ
(
⋅
)
表示激活函数,例如RELU,
H
(
l
)
∈
R
N
×
D
H^{(l)} \in R^{N \times D}
H
(
l
)
∈
R
N
×
D
是
l
l
l
层的激活矩阵,
H
(
0
)
=
X
H^{(0)} = X
H
(
0
)
=
X
,下面我们证明这种形式的传播规则可以由一个图的局部谱滤波的一阶近似得到。
谱图卷积
我们考虑图的谱卷积为一个信号
x
∈
R
N
x \in R^N
x
∈
R
N
在傅里叶域与一个滤波器
g
θ
=
d
i
a
g
(
θ
)
g_\theta = diag(\theta)
g
θ
=
d
i
a
g
(
θ
)
相乘:
g
θ
×
x
=
U
g
θ
U
T
x
g_\theta \times x = Ug_\theta U^Tx
g
θ
×
x
=
U
g
θ
U
T
x
,其中
U
U
U
是归一化后的拉普拉斯矩阵的特征向量矩阵
L
=
I
N
−
D
−
1
2
A
D
−
1
2
=
U
Λ
U
T
L = I_N – D^{-\frac{1}{2}}AD^{-\frac{1}{2}} = U\Lambda U^T
L
=
I
N
−
D
−
2
1
A
D
−
2
1
=
U
Λ
U
T
,其中
Λ
\Lambda
Λ
是特征值矩阵的对角矩阵,
U
T
x
U^Tx
U
T
x
是
x
x
x
的图傅里叶变换。我们可以把
g
θ
g_\theta
g
θ
理解为
L
L
L
的特征值的函数,即
g
θ
(
Λ
)
g_\theta(\Lambda)
g
θ
(
Λ
)
。上式的求解复杂度很高,于是我们将
g
θ
(
Λ
)
g_\theta(\Lambda)
g
θ
(
Λ
)
近似为一个切比雪夫多项展开式:
g
θ
′
(
Λ
)
≃
∑
k
=
0
K
θ
k
′
T
k
(
Λ
~
)
g_{\theta’}(\Lambda) \simeq \sum^K_{k=0}\theta’_kT_k(\widetilde{\Lambda})
g
θ
′
(
Λ
)
≃
k
=
0
∑
K
θ
k
′
T
k
(
Λ
)
其中
Λ
~
=
2
λ
m
a
x
Λ
−
I
N
\widetilde{\Lambda} = \frac{2}{\lambda{max}}\Lambda – I_N
Λ
=
λ
m
a
x
2
Λ
−
I
N
,
λ
m
a
x
\lambda_{max}
λ
m
a
x
表示
L
L
L
最大的特征值,
θ
′
∈
R
K
\theta’ \in R^K
θ
′
∈
R
K
是切比雪夫系数向量。切比雪夫多项式可以递归地定义为
T
k
(
x
)
=
2
x
T
k
−
1
(
x
)
−
T
k
−
2
(
x
)
T_k(x) = 2xT_{k-1}(x) – T_{k-2}(x)
T
k
(
x
)
=
2
x
T
k
−
1
(
x
)
−
T
k
−
2
(
x
)
,其中
T
0
(
x
)
=
1
,
T
1
(
x
)
=
x
T_0(x) = 1, T_1(x) = x
T
0
(
x
)
=
1
,
T
1
(
x
)
=
x
。
再看回我们的信号
x
x
x
和滤波器
g
θ
′
g_{\theta’}
g
θ
′
的卷积,我们现在有:
g
θ
×
x
≃
∑
k
=
0
K
θ
k
′
T
k
(
L
~
)
x
g_\theta \times x \simeq \sum^K_{k=0}\theta’_kT_k(\widetilde{L})x
g
θ
×
x
≃
k
=
0
∑
K
θ
k
′
T
k
(
L
)
x
其中
L
~
=
2
λ
m
a
x
L
−
I
N
\widetilde{L} = \frac{2}{\lambda_{max}}L-I_N
L
=
λ
m
a
x
2
L
−
I
N
,经过此番优化,上式的时间复杂度是与图中边的数量成线性关系的。
layer-wise线性模型
经过上一节的优化后,基于图卷积的神经网络模型就可以用上式中的卷积层进行堆叠了。现在,假设我们限制layer-wise卷积操作为
K
=
1
K=1
K
=
1
,那么就得到了一个线性模型。
通过堆叠多个这样的layer,我们就可以拟合很大一部分卷积滤波函数,并且不会受显式的参数形式(例如切比雪夫多项式)限制。我们期望这样的模型能够减轻大型图网络如社交网络,知识图谱和引用文献网络的局部过拟合问题。此外,这种层内线性的形式让我们能够构建更深的模型。
在这种GCN的线性形式中,我们进一步将
λ
m
a
x
\lambda_{max}
λ
m
a
x
近似为2,因为我们可以认为在训练阶段神经网络的参数会自动地适应这种变化。在这种近似下上式就可以简化为:
g
θ
′
×
x
≃
θ
0
′
x
+
θ
1
′
(
L
−
I
N
)
x
=
θ
0
′
x
−
θ
1
′
D
−
1
2
A
D
−
1
2
x
g_{\theta’} \times x \simeq \theta’_0x + \theta’_1(L – I_N)x = \theta’_0x – \theta’_1D^{-\frac{1}{2}}AD^{-\frac{1}{2}}x
g
θ
′
×
x
≃
θ
0
′
x
+
θ
1
′
(
L
−
I
N
)
x
=
θ
0
′
x
−
θ
1
′
D
−
2
1
A
D
−
2
1
x
filter参数可以在整个图中共享。
在实践中,我们可以进一步限定参数量来防止过拟合,同时也减少每一层的计算。于是我们的式子变为
g
θ
×
x
≃
θ
(
I
N
+
D
−
1
2
A
D
−
1
2
)
x
g_\theta \times x \simeq \theta(I_N + D^{-\frac{1}{2}}AD^{-\frac{1}{2}})x
g
θ
×
x
≃
θ
(
I
N
+
D
−
2
1
A
D
−
2
1
)
x
简化的过程是将
θ
=
θ
0
′
=
−
θ
1
′
\theta = \theta’_0 = -\theta_1′
θ
=
θ
0
′
=
−
θ
1
′
统一成一个参数。又因为重复求解
I
N
+
D
−
1
2
A
D
−
1
2
I_N + D^{-\frac{1}{2}}AD^{-\frac{1}{2}}
I
N
+
D
−
2
1
A
D
−
2
1
可能会导致数值不稳定从而导致梯度爆炸/消失,我们引入下式:
I
N
+
D
−
1
2
A
D
−
1
2
→
D
~
−
1
2
A
~
D
~
−
1
2
I_N + D^{-\frac{1}{2}}AD^{-\frac{1}{2}} \rightarrow \widetilde{D}^{-\frac{1}{2}}\widetilde{A}\widetilde{D}^{-\frac{1}{2}}
I
N
+
D
−
2
1
A
D
−
2
1
→
D
−
2
1
A
D
−
2
1
,其中
A
~
=
A
+
I
N
,
D
~
i
i
=
∑
j
A
~
i
j
\widetilde{A} = A + I_N, \widetilde{D}_{ii} = \sum_j\widetilde{A}_{ij}
A
=
A
+
I
N
,
D
i
i
=
∑
j
A
i
j
现在我们就可以将这个定义扩展到一个有
C
C
C
个通道和
F
F
F
个滤波器或特征map的信号
X
∈
R
N
×
C
X \in R^{N \times C}
X
∈
R
N
×
C
:
Z
=
D
~
−
1
2
A
~
D
~
−
1
2
X
Θ
Z = \widetilde{D}^{-\frac{1}{2}}\widetilde{A}\widetilde{D}^{-\frac{1}{2}}X\Theta
Z
=
D
−
2
1
A
D
−
2
1
X
Θ
其中
Θ
∈
R
C
×
F
\Theta \in R^{C \times F}
Θ
∈
R
C
×
F
是一个滤波器参数矩阵,
Z
∈
R
N
×
F
Z \in R^{N \times F}
Z
∈
R
N
×
F
是卷积后的信号矩阵。这种滤波操作的复杂度是
O
(
∣
ϵ
∣
F
C
)
O(|\epsilon|FC)
O
(
∣
ϵ
∣
F
C
)
半监督结点分类
在介绍了一种简单(?)又复杂的图上信息传播模型
f
(
X
,
A
)
f(X, A)
f
(
X
,
A
)
后,我们可以回到原本的分类问题上了。通过将模型同时作用在数据
X
X
X
和图的临界矩阵
A
A
A
上,我们可以不再依赖诸如图中的边仅表达结点相似性的假设。我们期望我们的模型能够在引文网络和知识图谱这种临界矩阵中包含数据
X
X
X
里没有的信息的场景有显著提升。模型的整体结构如下图所示:

举个栗子
下面我们考虑一个两层的GCN,它的邻接矩阵是一个对称矩阵
A
A
A
(二元或者带权重的),我们首先在预处理阶段计算出
A
^
=
D
~
−
1
2
A
~
D
~
−
1
2
\hat{A} = \widetilde{D}^{-\frac{1}{2}}\widetilde{A}\widetilde{D}^{-\frac{1}{2}}
A
^
=
D
−
2
1
A
D
−
2
1
,接下来我们模型的前向计算就是下面的形式:
Z
=
f
(
X
,
A
)
=
s
o
f
t
m
a
x
(
A
^
R
e
L
U
(
A
^
X
W
(
0
)
)
W
(
1
)
)
Z = f(X, A) = softmax(\hat{A}ReLU(\hat{A}XW^{(0)})W^{(1)})
Z
=
f
(
X
,
A
)
=
s
o
f
t
m
a
x
(
A
^
R
e
L
U
(
A
^
X
W
(
0
)
)
W
(
1
)
)
其中
W
(
0
)
∈
R
C
×
H
W^{(0)} \in R^{C \times H}
W
(
0
)
∈
R
C
×
H
是一个输入层到隐藏层的权重矩阵,
W
(
1
)
∈
R
H
×
F
W^{(1)} \in R^{H \times F}
W
(
1
)
∈
R
H
×
F
是一个隐藏层到输出层的权重矩阵。softmax函数是按行计算的,对于半监督学习的多分类任务,我们利用全部有标注的样本来计算交叉熵损失函数:
L
=
−
∑
l
∈
Y
L
∑
f
=
1
F
Y
l
f
l
n
Z
l
f
L = -\sum_{l \in Y_L}\sum^F_{f=1}Y_{lf}lnZ_{lf}
L
=
−
l
∈
Y
L
∑
f
=
1
∑
F
Y
l
f
l
n
Z
l
f
其中
Y
L
Y_L
Y
L
代表有标注的结点集合。
网络参数
W
(
0
)
W^{(0)}
W
(
0
)
和
W
(
1
)
W^{(1)}
W
(
1
)
用梯度下降来进行计算。具体实现中我们利用了tensorflow来获得了稀疏-稠密矩阵乘法效率上的优化。因为将邻接矩阵进行了稀疏表示,存储
A
A
A
的开销降低为
O
(
∣
ϵ
∣
)
O(|\epsilon|)
O
(
∣
ϵ
∣
)
,也就是与图中边的数量成线性关系,计算
f
(
X
,
A
)
f(X, A)
f
(
X
,
A
)
的复杂度为
O
(
∣
ϵ
∣
C
H
F
)
O(|\epsilon|CHF)
O
(
∣
ϵ
∣
C
H
F
)
,具体实现代码参考
作者的github
相关工作
基于图的半监督学习
近年来基于图的半监督学习可以大体分为两类:显式图拉普拉斯正则方法和基于embedding的方法。图拉普拉斯正则的典型工作包括label传播,manifold正则和深度半监督embedding。
近期研究者的注意力转向了skip-gram一系的图embedding方法,DeepWalk利用随机游走对图进行采样,利用对邻居的预测来学习结点embedding,LINE和node2vec继续扩展了DeepWalk。对于这些方法,random walk和半监督学习是两个独立进行的pipe。Planetoid通过在学习embedding的过程中注入label信息来改变了这一现状。
图神经网络
在图上构建神经网络的工作一开始是由Gori等人在2005年开展。Scarselli在2009年利用起了RNN,他们的方法持续地缩小原本的图作为传播函数,直到图结点缩减为指定数量。后来Li等人开始直接在原图上引用RNN。Duvenaud等人引入了一种类似于卷积的方式来进行图级别的分类。然而他们的方法不适用于大型图。
另一个相关的结点分类方法是将图局部地转化为序列,然后将序列输入一个一维卷积网络中。这种方法需要一个决定结点顺序的预处理过程。
实验
数据集
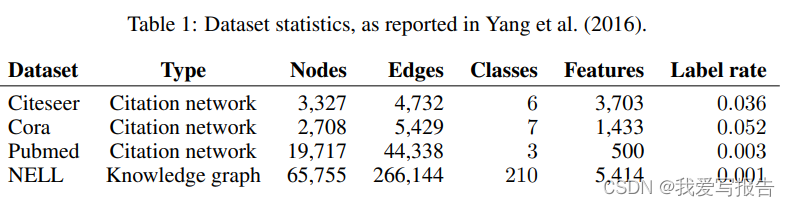
我们的数据集如上表所示,其中有两种数据——引用文献网络和知识图谱。在引用文献网络数据集中,结点是文献,边是引用链接。表中的Label rate表示在训练中用到的有标注的结点数量。
引用文献网络
我们的数据集中有三个引用文献网络:Citeseer, Cora和Pubmed。数据集中每篇文献都包含稀疏的词袋特征向量和一个文献间引用关系的list。我们将引用关系视作无向的边构建了一个二值的邻接矩阵A。每篇文献都有一个label,在训练中我们对每个类只使用20个label,但全部的特征向量都有被使用。
NELL
NELL是从一个知识图谱中抽取出来的数据集。知识图谱是一系列用有向的,有label的边连接起来的实体。对于NELL数据集我们进行了一个预处理——对每个实体对
(
e
1
,
r
,
e
2
)
(e_1, r, e_2)
(
e
1
,
r
,
e
2
)
指定了相互分离的关系结点
r
1
r_1
r
1
和
r
2
r_2
r
2
,于是实体对就可以表示为
(
e
1
,
r
1
)
(e_1, r_1)
(
e
1
,
r
1
)
和
(
e
2
,
r
2
)
(e_2, r_2)
(
e
2
,
r
2
)
。实体结点用稀疏的特征向量表示,我们通过指定一个one-hot的关系结点表示将NELL的特征扩展到了61278维。我们的半监督学习任务考虑了一个非常极端的情况——每个类只有一个标注样本。我们将图的邻接矩阵构建成一个二值矩阵,即如果
i
i
i
和
j
j
j
之间有大于等于一条边相连,则
A
i
j
=
1
A_{ij}=1
A
i
j
=
1
随机图
我们利用随机生成的图数据集来评估我们的训练性能。对于一个有N个结点的数据集我们创建一个均匀采样的有2N个边的图,用单位矩阵作为输入的特征矩阵
X
X
X
,并且为全部结点服务label
Y
i
=
1
Y_i=1
Y
i
=
1
实验设置
我们训练一个两层的GCN,用一个有1000个样本的测试集评估预测的准确性(acc)。我们与Yang等人采用相同的数据集划分方法,在调参(dropout, L2正则参数)过程中使用一个有500个标注样本的验证集。在训练阶段,我们利用Adam优化器训练最多200轮,学习率是0.01,进行了窗口大小为10的早停。如果验证集loss超过10轮没有下降则停止训练。我们用Glorot&Bengio在10年提出的方法来初始化权重。
Baseline
我们的baseline方法包括:label propagation, SemiEmb,manifold regularization,DeepWalk,此外我们还与ICA方法进行了对比,这种方法使用两个逻辑回归,分别以结点特征和局部图的特征为输入,并将两个逻辑回归的输出进行融合得到最终的分类。最后我们与Yang等人的方法Planetoid进行了对比。
实验结果
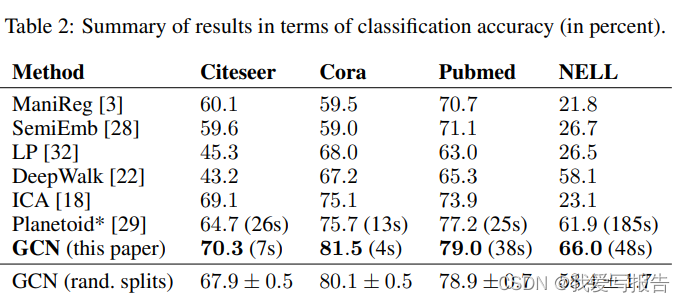
实验结果如上表所示,数字代表分类acc。
下表列出了GCN在不同的传播函数下的表现。

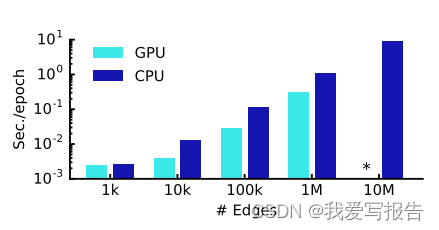
下图是在不同边数量的情况下,随机图的训练性能