博客

写在前面：最速下降法求解函数极小值的理论部分已经写在上一篇文章中，这篇文章直接进行具体问题的求解并附上matlab代码。

1.题目

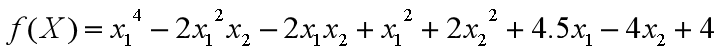
设初始点为[x1 x2]=[-2.5 4.5] ，ε≤0.01，求目标函数的极小值。

2.matlab代码

2.1主函数

syms x1 x2 s; %声明符号变量

f1 =  x1^4 - 2*x1^2*x2 - 2*x1*x2 + x1^2 + 2*x2^2 + 4.5*x1 - 4*x2 + 4;%设定目标函数

k=steepest_descent(f1,x1,x2,s,[-2.5,4.25],10^(-2));  %设定起始点[x1 x2]=[-2.5,4.25]和精度10^(-2)

result_string=sprintf('在 %d 次迭代后求出极小值\n',k);%在迭代多少次之后求出极小值
disp(result_string);

2.2调用函数

function   k = steepest_descent(f,x1,x2,s,start_point,thereshold) 
    
    k = 0;%迭代次数赋值初始化
    
    grad_f = [diff(f,x1) diff(f,x2)]; %计算f的梯度
    
    delta = subs(grad_f,[x1,x2],[start_point(1),start_point(2)]);
    %计算起点的梯度
    
    step=1; %设置初始步长为1
    
    current_point = start_point;%起点值赋给当前点
    
    %最速下降法的主循环，判断条件为：梯度的模与所给精度值进行比较
    while norm(delta) > thereshold  
        
        k = k + 1;%迭代次数+1
        
        %一维探索 求最优步长（此时方向已知，步长s为变量）
        x_next = [current_point(1),current_point(2)] - s* delta/norm(delta);% 计算x（k+1）点，其中步长s为变量 
        f_val = subs(f,[x1,x2],[x_next(1),x_next(2)]);% 将x值带入目标函数中
        step = abs(double(solve(diff(f_val,s)))); % 对s求一阶导，并加绝对值符号，得到最优步长的绝对值
        step = step(1);%更新步长
        
        %计算x（k+1）点
        current_point = double([current_point(1),current_point(2)] - step * delta/norm(delta));
        
        %计算x（k+1）点的梯度值
        delta = subs(grad_f,[x1,x2],[current_point(1),current_point(2)]);
        
        %计算函数值
        f_value = double(subs(f,[x1,x2],[current_point(1),current_point(2)]));
        
        %输出迭代计算过程
        result_string=sprintf('k=%d, x1=%.6f, x2=%.6f, step=%.6f f(x1,x2)=%.6f',...
        k,current_point(1),current_point(2),step,f_value);
        disp(result_string);
        
    end
end

（使用代码时，只需要把主函数中目标函数 ；起始点； 精度，重新设置成你所需要的就可运行。）

2.3运行结果

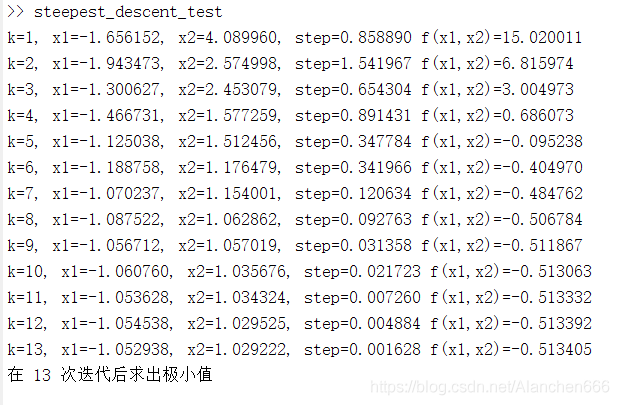
3.分析

将收敛条件由ε≤0.01改为ε≤10^(-6)，运行结果如下：



可以看出，利用最速下降法求函数极小值时，在最初几步迭代中函数值下降很快，但当函数值

越接近理论极小值时，函数值下降的越慢

，同时，越接近理论极小值时，步长也越小，因此最速下降法的收敛速度并不快，这是因为函数在x（k）点处的

负梯度方向为其最速下降方向仅仅是针对该点处而言

，，一旦离开该点，原先方向就不是最速下降方向了。

最速下降方向只是针对当前的计算点而言，并非是全局的最速下降方向

最速下降法优点：对初始点选择要求低，远离极值点时收敛速度快

缺点：越逼近理论极小值，收敛速度越慢