博客

基本思想

从出发节点开始访问，然后去访问该节点的所有相邻节点，访问完该节点的所有相邻节点后，以相邻节点中的第一个节点为起点，继续去访问其所有相邻节点，反复持续该过程直到图中所有节点均被访问过退出。这样一来，图的访问顺序就是一个横向的访问顺序。

和广度优先搜索一样，我们将要访问的节点称为头节点，相邻节点称为表节点；头节点中存储数据和第一个表节点，表节点中存储头节点的下标和头节点的下一个相邻节点；头节点使用顺序（链表）存储，表节点使用链表存储。

广度优先搜索和深度优先搜索的区别其实就是在于遍历策略的不同，

广度优先搜索是访问完每一个节点，就去访问该节点的所有相邻节点；而深度优先遍历是每访问一个节点，就去访问该节点的第一个相邻节点

。

如下图，其广度优先搜索顺序就是

v1, v2, v3, v4, v5, v6, v7, v8

，注意：广度优先搜索的顺序也不是唯一的，和深度优先搜索一样，取决于访问起点和表节点的顺序。

实现思路

• 访问头节点，并将该头节点标记为以访问过
• 访问头节点的所有表节点，这里需要循环
• 然后以第一个表节点为起点，继续以上两步操作直到访问完所有头节点，这里需要递归
• 我们还需要使用到队列，来存储每次访问过程中所有表节点中的第一个表节点，也就是我们下一次访问的起点

代码实现

定义头节点和表节点

//头节点
public class HNode<T> {

    public T data; //数据域
    public boolean isVisit; //标识该头节点是否已经被访问过
    public TNode firstArc; //指针域，指向第一个表节点

    public HNode(T data) {
        this.data = data;
    }

    public HNode() {
    }

    @Override
    public String toString() {
        return "HNode{" +
                "data=" + data +
                ", isVisit=" + isVisit +
                ", firstArc=" + firstArc +
                '}';
    }
}

//表节点
class TNode {

    public int hNodeIndex;//存储头节点下标
    public TNode nextArc; //指针域，指向下一个相邻的表节点

    public TNode(int hNodeIndex) {
        this.hNodeIndex = hNodeIndex;
    }

}

定义一个 Graph 类，一个Graph类就表示一个图

public class Graph {

    private HNode[] vertices; //存储头节点

    //用于广度优先搜索
    private LinkedQueue<HNode> queue = new LinkedQueue();

    public Graph(HNode[] vertices) {
        this.vertices = vertices;
    }

    //构建图
    public void build(Object data) {

    }

    //广度优先搜索
    //index为遍历起点
    public void wfs(int index) {
        //访问头节点
        System.out.println(vertices[index].data);
        //设置当前头节点为已访问
        vertices[index].isVisit = true;
        //当前头节点入队列
        queue.enQueue(vertices[index]);
        //不断从队列中取出首节点，直到队列为空
        while (!queue.isEmpty()) {
            //开始遍历
            //获取第一个表节点
            TNode tNode = queue.outQueue().getData().firstArc;
            //只要当前表节点不为空，就说明该头节点的表节点没有遍历结束，我们就一直循环下去
            while (tNode != null) {
                //只要当前表节点对应的头节点没有被访问过，就进行访问
                if (!(vertices[tNode.hNodeIndex].isVisit)) {
                    System.out.println(vertices[tNode.hNodeIndex].data);
                    //设置当前头节点为已访问
                    vertices[tNode.hNodeIndex].isVisit = true;
                    //访问完节点后，将该节点入队列
                    queue.enQueue(vertices[tNode.hNodeIndex]);
                }
                //hNode后移
                tNode = tNode.nextArc;
            }
        }
   	}
}

再main方法中测试

public class WFSDemo {

    public static void main(String[] args) {

        HNode[] nodes = new HNode[5];

        for (int i = 0; i < nodes.length; i++) {
            HNode<String> node = new HNode<>("张三-" + (i + 1));
            nodes[i] = node;
        }

        TNode node1 = new TNode(2);
        node1.nextArc = new TNode(3);
        nodes[0].firstArc = node1;
        TNode node2 = new TNode(0);
        node2.nextArc = new TNode(4);
        nodes[1].firstArc = node2;
        TNode node3 = new TNode(1);
        node3.nextArc = new TNode(3);
        nodes[2].firstArc = node3;
        TNode node4 = new TNode(0);
        node4.nextArc = new TNode(1);
        nodes[3].firstArc = node4;
        TNode node5 = new TNode(3);
        node5.nextArc = new TNode(2);
        nodes[4].firstArc = node5;

        for (HNode node : nodes) {
            System.out.println(node);
        }

        Graph graph = new Graph(nodes);

        System.out.println("--------------广度优先搜索--------------");
        graph.wfs(0);
        
    }

}

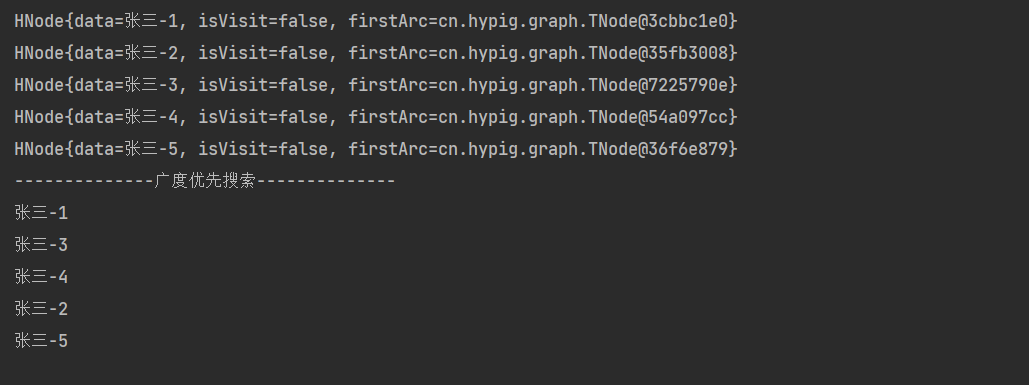
测试结果