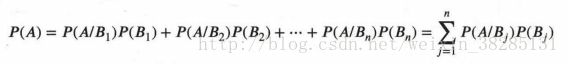在理解贝叶斯之前需要先了解一下条件概率和全概率,这样才能更好地理解贝叶斯定理
一丶条件概率
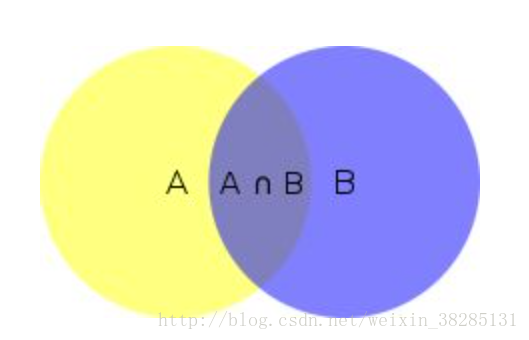
条件概率定义:已知事件A发生的条件下,另一个事件B发生的概率成为条件概率,即为P(B|A)
如图A∩B那一部分的发生的概率即为P(AB),
P(AB)=发生A的概率*发生A之后发生B的概率=发生B的概率*发生B之后发生A的概率
即:
P(AB)=P(A)*P(B|A)=P(B)*P(A|B)
所以
条件概率公式
:
P(B|A)=P(AB)/P(A)=P(B)*P(A|B)/P(A)
二丶全概率公式
全概率公式就是在样本空间E中,有一个事件A,而样本空间被划分为多个子空间B1,B2,B3…….,对于每一个子空间Bi,发生A事件的概率为:
P(A)=P(Bi)*P(A|Bi) i=1,2,3......n
也就是:发生Bi的概率*Bi中发生A的概率
那么整个样本空间E中发生A的概率即为:每一个样本子空间中发生A的概率的总和:
P(A)=P(B1)*P(A|B1)+P(B2)*P(A|B2)+.............+P(Bn)*P(A|Bn)
以上就是
全概率公式
,也可以写作:
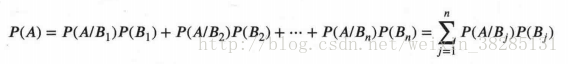
全概率公式就是求一个事件在整个样本中发生的概率
三丶贝叶斯定理
贝叶斯定理不同的是,他是已知一个事件在整个样本中发生的概率之后,然后求另一个时间发生的概率
比如在A时间发生的情况下,它属于Bi子样本空间的概率P(Bi|A),那么我们就可以根据
条件概率公式
来求
发生a事件概率*发生a事件且a时间发生在Bi子样本的概率=发生Bi的概率*发生Bi之后发生a的概率
即为:**P(Bi|A)*P(A)=P(Bi)*P(A|Bi)**
然后根据全概率公式:
所以:
P(Bi/A)=P(Bi)*P(A|Bi)/P(A)
把P(A)带入上面的式子,可得
贝叶斯公式
:
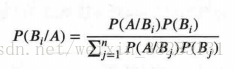
下面我们举个例子:
在这一系列数据中计算出在第三个子数据集中发生1事件的概率:
python实现:
#创建一个虚拟的数据
def c_data():
dataset=[
[1,2,3,5,1],#数据中包含四个子数据
[1,2,1,1,8,8],
[1,7,2,3,5],
[4,8,9,1,1,8,9,3]
]
return dataset
#计算某一事件A发生的全概率
def compute_prob(dataset,event):
#发生的概率
prob_event=0.0
for sub_dataset in dataset:
prob_sub=1/len(dataset)#该子集发生的概率
num=len(sub_dataset)#子集的数据个数
data_dict = {}#创建一个字典
for data in sub_dataset:
prob=0.0
if data in data_dict:
data_dict[data]+=1
else:
data_dict[data]=1
if event in data_dict:
prob+=data_dict[event]/num#事件在该子集中的出现概率
data_dict.clear()#清空字典用于下一个子集
else:
print("没有该事件")
prob_event+=prob*prob_sub #子集发生概率*自己中事件发生概率
return prob_event#返回事件的全概率
#计算事件A发生条件下第几个子空间sub_dataset发生的概率
def comnpute_prob_sub_dataset(dataset,sub_dataset_id,event):
prob_sub_dataset=1/len(dataset)#发生在该子空间的概率
print("发生在该子空间中的概率:%f"%prob_sub_dataset)
event_num=dataset[sub_dataset_id].count(event)#该事件在子空间中出现的次数
prob_sub_dataset_event=event_num/len(dataset[sub_dataset_id])#事件在子空间中发生的概率
print("在改子空间中发生事件的概率:%f"%prob_sub_dataset_event)
prob_event=compute_prob(dataset,event=event)
print("整个样本发生事件的概率:%f"%prob_event)
prob_sub_dataset=(prob_sub_dataset*prob_sub_dataset_event)/prob_event#事件发生在某一子集中的概率
print("概率为:%f"%prob_sub_dataset)
return prob_sub_dataset
dataset=c_data()
comnpute_prob_sub_dataset(dataset,sub_dataset_id=2,event=1)#1出现在第三个子集中的概率
结果:
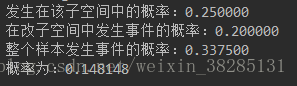
这只是一个简单的例子,可以笔算试一下 看看是不是这个结果。代码还能优化,自己才疏学浅,也是个渣