前言
或(|)、且(&)、反(~)、异或(^)等是计算机语言中常见的二进制运算符,想要对这几种运算的计算机实现理解的比较透彻,首先需要知道,数在计算机中是如何表示的。
目录
1、数的二进制表示
1.1 二进制和符号位
1.2 原码、反码、补码
2、位运算
2.1 异或运算 ^
2.2 或运算 |
2.3 且运算 &
2.4 取反运算 ~
2.5 位移运算
2.6 负号运算
正文
1 、数的二进制表示
1.1 二进制和符号位
我们日常使用的数字表示方法是十进制,每一位可以取0,1,2,…,9,满10进1,每一位都有其对应的单位(从低到高分别是:个,十,百,千,万… …)。计算机中最基本的存储单元是位(bit),每一个位只能存储0或1,满2进1,同样的,每一位都有其对应的单位(从低到高分别是:
,
,
……)。下面给出一个例子方便理解:

在二进制表示中,为了区分正数和负数,把最高位当作符号位,0表示正数,1表示负数,绝对值相等的正负数的非符号位相等。比如,使用8位二进制数时,第8位为符号位:
十进制7的8位二进制 0000 0111
十进制-7的8位二进制 1000 0111
1.2 原码、反码、补码(8位为例)
原码
正数原码为其二进制
比如:
1
的原码
0000 0001
,
5
的原码
0000 0101
负数的原码为其绝对值二进制表示加符号位
比如:
-1
的原码
1000 0001, -5
的原码
1000 0101
反码
正数反码是其原码
比如:
1
的反码
0000 0001
,
5
的反码
0000 0101
负数的反码 由其原码符号位不变,其余位和
1
取异或
(1-
各个位的值
)
得到
比如:
-1
的反码
1111 1110, -5
的反码
1111 1010
补码
正数补码为其原码
比如:
1
的补码
0000 0001
,
5
的补码
0000 0101
负数的补码为其反码
+1
比如:
-1
的补码
1111 1111, -5
的补码
1111 1011
2、位运算(计算机中,数的表示使用的是补码)
2.1 异或运算 ^
1^0 = 1
,
0^1 = 1
,
1^1=0
,
0^0 = 0(二进制)
比如:
1^5 = 0000 0001 ^ 0000 0101 = 0000 0100 = 4
(-1)^(-5) = 1111 1111 ^ 1111 1011 = 0000 0100 = 4
2.2或运算 |
1|0 = 1
,
0|1 = 1
,
1|1=1
, 0|0 = 0 (二进制)
比如:
1|5 = 0000 0001 | 0000 0101 = 0000 0101 = 5
(-1)|(-5) = 1111 1111 | 1111 1011 = 1111 1111 = -1
2.3 且运算 &
1
&
0 = 0
,
0
&
1 = 0
,
1
&
1=1
,
0
&
0 = 0 (二进制)
比如:
1&5 = 0000 0001
&
0000 0101 = 0000 0001 = 1
(-1)&(-5) = 1111 1111
&
1111 1011 = 1111 1011 = -5
2.4 取反运算 ~
~1 = 0, ~0 = 1 (二进制)
比如:
~1
= ~(0000 0001)
= 1111
1110 = -2,
~5
的
=
1111 1010 = -6
~(-1)
= ~(1111 1111) =
0000 0000 = 0, ~(-5) = 0000 0100 = 4
2.5 位移运算
左移(
<
<
)
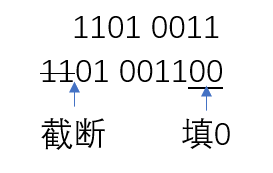
把二进制的每一位向左移动,超出存储空间的截断(丢掉),空缺出来的位填
0
比如
:
1101 0011 << 2 = 0100 1100
右移
(
>
>
)
把二进制的每一位向
右
移动,超出存储空间的截断(丢掉),空缺出来的位填
0
•
比如:1101 0011 >> 3 = 0001 1010

2.6 负号运算
(-n) = (~n) + 1
比如 -1 = ~0000 0001 + 1 = 1111 1110 + 1 = 1111 1111 = -1
-(-1) = ~(-1)+1 = ~1111 1111 + 1 = 0000 0000 + 1 = 0000 0001 = 1
注意C++中运算的优先级
“~”
>
“*,/,%”
>
“+,-”
>
“<<,>>”
>
“&”
>
“^”
>
“|”
按位取反 > 乘、除、取余 > 加、减 > 位移 > 且 > 异或 > 或
参考:
负数和正数的存储方式。_mlove编程-CSDN博客_负数的存储方式