5.5

5.5 Media applications that play audio or video fi les are part of a class of workloads called “streaming” workloads; i.e., they bring in large amounts of data but do not reuse much of it. Consider a video streaming workload that accesses a 512 KiB working set sequentially with the following address stream:

0, 2, 4, 6, 8, 10, 12, 14, 16,

5.5.1 [5] <§§5.4, 5.8> Assume a 64 KiB direct-mapped cache with a 32-byte block. What is the miss rate for the address stream above? How is this miss rate sensitive to the size of the cache or the working set? How would you categorize the misses this workload is experiencing, based on the 3C model?

指定地址为字节地址，每一组的16次访问会映射到相同的32字节块，cache的失效率为

16

\frac{1}{16}

$\frac{1}{16}$
所有的失效都是必然的，失效率对缓存大小或工作集大小不敏感；对访问模式和块大小敏感

5.5.2 [5] <§§5.1, 5.8> Re-compute the miss rate when the cache block size is 16 bytes, 64 bytes, and 128 bytes. What kind of locality is this workload exploiting?

分别为

$\frac{1}{8} 8 1 $
$\frac{1}{32} 32 1 $
$\frac{1}{64} 64 1 $

工作负载正在利用

空间

局限性

5.5.3 [10] <§5.13>“Prefetching” is a technique that leverages predictable address patterns to speculatively bring in additional cache blocks when a particular cache block is accessed. One example of prefetching is a stream buff er that prefetches sequentially adjacent cache blocks into a separate buff er when a particular cache block is brought in. If the data is found in the prefetch buff er, it is considered as a hit and moved into the cache and the next cache block is prefetched. Assume a two-entry stream buff er and assume that the cache latency is such that a cache block can be loaded before the computation on the previous cache block is completed. What is the miss rate for the address stream above?

Cache block size (B) can aff ect both miss rate and miss latency. Assuming a 1-CPI machine with an average of 1.35 references (both instruction and data) per instruction,help fi nd the optimal block size given the following miss rates for various block sizes.

8: 4% 
16: 3% 
32: 2% 
64: 1.5% 
128: 1%

相邻的cache块如果存在预取缓冲区中，那么不会有缺失率

5.5.4 [10] <§5.3> What is the optimal block size for a miss latency of 20×B cycles?

计算

average memory access time

块大小为8的情况
$4\%\times(20\times8)=6.4 4% × ( 20 × 8 ) = 6.4$
块大小为16的情况
$3\%\times(20\times16)=9.6 3% × ( 20 × 16 ) = 9.6$
块大小为32的情况
$2\%\times(20\times32)=12.8 2% × ( 20 × 32 ) = 12.8$
块大小为64的情况
$1.5\%\times(20\times64)=19.2 1.5% × ( 20 × 64 ) = 19.2$
块大小为128的情况
$1\%\times(20\times128)=25.6 1% × ( 20 × 128 ) = 25.6$

选第一种情况

5.5.5 [10] <§5.3> What is the optimal block size for a miss latency of 24+B cycles?

块大小为8的情况
$4\%\times(20+8)=1.28 4% × ( 20 + 8 ) = 1.28$
块大小为16的情况
$3\%\times(20+16)=1.20 3% × ( 20 + 16 ) = 1.20$
块大小为32的情况
$2\%\times(20+32)=1.12 2% × ( 20 + 32 ) = 1.12$
块大小为64的情况
$1.5\%\times(20+64)=1.32 1.5% × ( 20 + 64 ) = 1.32$
块大小为128的情况
$1\%\times(20+128)=1.52 1% × ( 20 + 128 ) = 1.52$

第三种情况最好

5.5.6 [10] <§5.3> For constant miss latency, what is the optimal block size?

恒定值选取128即可，失效率最小

5.6 In this exercise, we will look at the diff erent ways capacity aff ects overall performance. In general, cache access time is proportional to capacity. Assume that main memory accesses take 70 ns and that memory accesses are 36% of all instructions. Th e following table shows data for L1 caches attached to each of two processors, P1 and P2.

	L1 Size	L1 Miss Rate	L1 Hit Time
P1	2 KiB	8.0%	0.66 ns
P2	4 KiB	6.0%	0.90 ns

5.6.1 [5] <§5.4> Assuming that the L1 hit time determines the cycle times for P1 and P2, what are their respective clock rates?

5.6.2 [5] <§5.4> What is the Average Memory Access Time for P1 and P2?

假定失效的时候已经探索过一边cache了，也有0.66的损耗

P1的AMAT
$8\%\times 70ns = 6.26ns 0.66 n s + 8% × 70 n s = 6.26 n s$
P2的AMAT
$6\%\times 70ns = 5.1ns 0.9 n s + 6% × 70 n s = 5.1 n s$

5.6.3 [5] <§5.4> Assuming a base CPI of 1.0 without any memory stalls, what is the total CPI for P1 and P2? Which processor is faster?

题目没说时钟周期和时钟频率，这里就假设

访问一级cache认为是一个周期（答案的CPI不知道数据咋来的）

P1的CPI
$\times 0.64 + 0.36\times(6.26/0.66)= 4.05 1 × 0.64 + 0.36 × ( 6.26/0.66 ) = 4.05$
P2的CPI
$\times 0.64 + 0.36\times(5.1/0.9)= 2.68 1 × 0.64 + 0.36 × ( 5.1/0.9 ) = 2.68$

P2更快一点

For the next three problems, we will consider the addition of an L2 cache to P1 to presumably make up for its limited L1 cache capacity. Use the L1 cache capacities and hit times from the previous table when solving these problems. Th e L2 miss rate indicated is its local miss rate.

L2 Size	L2 Miss Rate	L2 Hit Time
1 MiB	95%	5.62 ns

5.6.4 [10] <§5.4> What is the AMAT for P1 with the addition of an L2 cache? Is the AMAT better or worse with the L2 cache?

P1的AMAT

0.08

(

5.62

0.95

)

6.4296

0.66ns + 0.08\times(5.62 + 0.95\times 70 ) = 6.4296ns

$0.66 n s + 0.08 \times (5.62 + 0.95 \times 70) = 6.4296 n s$

AMAT上升，CPI上升，性能更差

5.6.5 [5] <§5.4> Assuming a base CPI of 1.0 without any memory stalls, what is the total CPI for P1 with the addition of an L2 cache?

0.64

0.36

(

6.4296

0.66

)

4.14705

1 \times 0.64 + 0.36\times(6.4296/0.66)= 4.14705

$1 \times 0.64 + 0.36 \times (6.4296/0.66) = 4.14705$

5.6.6 [10] <§5.4> Which processor is faster, now that P1 has an L2 cache? If P1 is faster, what miss rate would P2 need in its L1 cache to match P1’s performance? If P2 is faster, what miss rate would P1 need in its L1 cache to match P2’s performance?

P1的AMAT为5.6.4 6.4296ns
P2没加2级cache，AMAT数据同5.6.2：5.1ns

想让P1匹配P2的表现

(

5.62

0.95

)

5.1

0.66ns + x\times(5.62 + 0.95\times 70 ) = 5.1ns

$0.66 n s + x \times (5.62 + 0.95 \times 70) = 5.1 n s$

4.44

72.12

6.156

x = \frac{4.44}{72.12} = 6.156\%

$x = \frac{4.44}{72.12} = 6.156%$

5.7 Th is exercise examines the impact of diff erent cache designs, specifi cally comparing associative caches to the direct-mapped caches from Section 5.4. For these exercises, refer to the address stream shown in Exercise 5.2.

5.7.1 [10] <§5.4> Using the sequence of references from Exercise 5.2, show the final cache contents for a three-way set associative cache with two-word blocks and a total size of 24 words. Use LRU replacement. For each reference identify the index bits, the tag bits, the block off set bits, and if it is a hit or a miss.

5.7.1这里写的时候遗漏了一个block是两个字大小，所以下面的错了，应该是分成 422来分析而不是 431，但是笔者懒得修正了，请按照实际情况修改

cache容量24字，三路相连，所以映射为

24/3=8

$24/3 = 8$

个block，所以索引字段m = 3

这里应该是24/3/2=4， m =2

字地址	二进制地址	标签index	索引tag	命中或失效
3	0000 001 1	$0000_{(2)} 000 0 ( 2 ) = 0$	$001_{(2)} 00 1 ( 2 ) = 1$	Miss
180	1011 010 0	$1011_{(2)} 101 1 ( 2 ) = 11$	$001_{(2)} 00 1 ( 2 ) = 2$	Miss
43	0010 101 1	$0010_{(2)} 001 0 ( 2 ) = 2$	$101_{(2)} 10 1 ( 2 ) = 5$	Miss
2	0000 001 0	$0000_{(2)} 000 0 ( 2 ) = 0$	$001_{(2)} 00 1 ( 2 ) = 1$	Hit(第一行)
191	1011 111 1	$1011_{(2)} 101 1 ( 2 ) = 11$	$111_{(2)} 11 1 ( 2 ) = 7$	Miss
88	0101 100 0	$0101_{(2)} 010 1 ( 2 ) = 5$	$100_{(2)} 10 0 ( 2 ) = 4$	Miss
190	1011 111 0	$1011_{(2)} 101 1 ( 2 ) = 11$	$111_{(2)} 11 1 ( 2 ) = 7$	Hit（第五行）
14	0000 111 1	$0000_{(2)} 000 0 ( 2 ) = 0$	$111_{(2)} 11 1 ( 2 ) = 7$	Miss
181	1011 010 1	$1011_{(2)} 101 1 ( 2 ) = 11$	$010_{(2)} 01 0 ( 2 ) = 2$	Hit（第二行）
44	0010 110 0	$0010_{(2)} 001 0 ( 2 ) = 2$	$110_{(2)} 11 0 ( 2 ) = 6$	Miss
186	1011 010 1	$1011_{(2)} 101 1 ( 2 ) = 11$	$110_{(2)} 11 0 ( 2 ) = 5$	Miss
253	1111 110 1	$1111_{(2)} 111 1 ( 2 ) = 15$	$110_{(2)} 11 0 ( 2 ) = 7$	Miss

映射如下

访问3后：
    (1->0)
访问180后：
    (1->0) (2->11)
访问43后：
    (1->0) (2->11) (5->2)
访问2后：
    (1->0) (2->11) (5->2)
访问191后：
    (1->0) (2->11) (5->2) (7->11)
访问88后：
    (1->0) (2->11) (4->5) (5->2) (7->11)
访问190后：
    (1->0) (2->11) (4->5) (5->2) (7->11)
访问14后：
    (1->0) (2->11) (4->5) (5->2) (7->0,7->11)
    #这里把7->11的映射往后挪了
访问181后：
    (1->0) (2->11) (4->5) (5->2) (7->0,7->11)
访问44后：
    (1->0) (2->11) (4->5) (5->2) (6->2) (7->0,7->11)
访问186后：
    (1->0) (2->11) (4->5) (5->11, 5->2) (6->2) (7->0,7->11)
访问253后：
    (1->0) (2->11) (4->5) (5->11, 5->2) (6->2) (7->15, 7->0,7->11)

5.7.2 [10] <§5.4> Using the references from Exercise 5.2, show the fi nal cache contents for a fully associative cache with one-word blocks and a total size of 8 words. Use LRU replacement. For each reference identify the index bits, the tag bits, and if it is a hit or a miss.

cache是全关联，所以直接全部堆起来就行了,根本没有index

Tag	H/M	映射
3	M	3
180	M	3,180
43	M	3,180,43
2	M	3,180,43,2
191	M	3,180,43,2,191
88	M	3,180,43,2,191,88
190	M	3,180,43,2,191,88,190
14	M	3,180,43,2,191,88,190,14
181	M	181,180,43,2,191,88,190,14
44	M	181,44,43,2,191,88,190,14
186	M	181,44,186,2,191,88,190,14
253	M	181,44,186,253,191,88,190,14

5.7.3 [15] <§5.4> Using the references from Exercise 5.2, what is the miss rate for a fully associative cache with two-word blocks and a total size of 8 words, using LRU replacement? What is the miss rate using MRU (most recently used) replacement? Finally what is the best possible miss rate for this cache, given any replacement policy?

储存方式同上，只不过块改成2个字

又出问题，这里根据题意只有四个块，所以有便映射最多只能放四个，而不是八个，所以下面的表错了

data	Tag	H/M	映射
3	1	M	1
180	1	M	1,90
43	21	M	1,90,21
2	1	M	90,21,1
191	95	M	90,21,1,95
88	44	M	90,21,1,95,44
190	95	H	90,21,1,44,95
14	7	M	90,21,1,44,95,7
180	90	H	21,1,44,95,7,90
44	22	M	21,1,44,95,7,90,22
186	93	M	21,1,44,95,7,90,22,93
253	126	M	1,44,95,7,90,22,93,126

缺失率

9/12=75\%

$9/12 = 75%$

如果使用MRU算法，那在访问253的时候，被移除的数据应该为93，缺失率和LRU一致，并且这就是最好的缺失率，因为除了21并没有从cache中移除的数据

Multilevel caching is an important technique to overcome the limited amount of space that a fi rst level cache can provide while still maintaining its speed. Consider a processor with the following parameters:

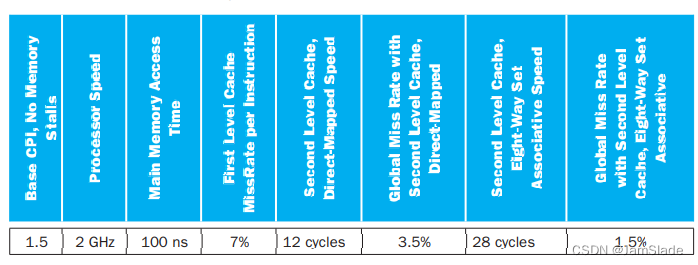
在这里插入图片描述

5.7.4 [10] <§5.4> Calculate the CPI for the processor in the table using: 1) only a fi rst level cache, 2) a second level direct-mapped cache, and 3) a second level eight-way set associative cache. How do these numbers change if main memory access time is doubled? If it is cut in half?

只有一级：失效的CPI

×

100

n

s

/

0.5

n

s

=

14

0.07\times 100ns / 0.5ns = 14

$0.07 \times 100 n s /0.5 n s = 14$
二级映射：

×

(

12

∗

0.5

n

s

+

0.035

×

100

n

s

)

/

0.5

n

s

=

1.33

0.07\times(12*0.5ns + 0.035\times 100ns) / 0.5ns = 1.33

$0.07 \times (12 * 0.5 n s + 0.035 \times 100 n s) /0.5 n s = 1.33$
八路组相连

×

(

28

×

0.5

n

s

+

0.015

×

100

n

s

)

/

0.5

n

s

=

2.17

0.07\times(28\times 0.5ns + 0.015\times 100ns) / 0.5ns=2.17

$0.07 \times (28 \times 0.5 n s + 0.015 \times 100 n s) /0.5 n s = 2.17$

时间加倍

只有一级：失效的CPI

×

200

n

s

/

0.5

n

s

=

28

0.07\times 200ns / 0.5ns = 28

$0.07 \times 200 n s /0.5 n s = 28$
二级映射：

×

(

12

∗

0.5

n

s

+

0.035

×

200

n

s

)

/

0.5

n

s

=

1.82

0.07\times(12*0.5ns + 0.035\times 200ns) / 0.5ns = 1.82

$0.07 \times (12 * 0.5 n s + 0.035 \times 200 n s) /0.5 n s = 1.82$
八路组相连

×

(

28

×

0.5

n

s

+

0.015

×

200

n

s

)

/

0.5

n

s

=

2.38

0.07\times(28\times 0.5ns + 0.015\times 200ns) / 0.5ns=2.38

$0.07 \times (28 \times 0.5 n s + 0.015 \times 200 n s) /0.5 n s = 2.38$

时间缩短

只有一级：失效的CPI

×

50

n

s

/

0.5

n

s

=

7

0.07\times 50ns / 0.5ns = 7

$0.07 \times 50 n s /0.5 n s = 7$
二级映射：

×

(

12

∗

0.5

n

s

+

0.035

×

50

n

s

)

/

0.5

n

s

=

1.085

0.07\times(12*0.5ns + 0.035\times 50ns) / 0.5ns = 1.085

$0.07 \times (12 * 0.5 n s + 0.035 \times 50 n s) /0.5 n s = 1.085$
八路组相连

×

(

28

×

0.5

n

s

+

0.015

×

50

n

s

)

/

0.5

n

s

=

2.065

0.07\times(28\times 0.5ns + 0.015\times 50ns) / 0.5ns=2.065

$0.07 \times (28 \times 0.5 n s + 0.015 \times 50 n s) /0.5 n s = 2.065$

5.7.5 [10] <§5.4> It is possible to have an even greater cache hierarchy than two levels. Given the processor above with a second level, direct-mapped cache, a designer wants to add a third level cache that takes 50 cycles to access and will reduce the global miss rate to 1.3%. Would this provide better performance? In general, what are the advantages and disadvantages of adding a third level cache?

三级cache的CPI失效计算如下

(

0.5

0.035

(

0.5

0.013

100

0.5

)

0.5

0.965685

0.07\times(12\times0.5ns + 0.035\times(50\times 0.5ns+0.013\times100\times 0.5ns)) /0.5ns = 0.965685

$0.07 \times (12 \times 0.5 n s + 0.035 \times (50 \times 0.5 n s + 0.013 \times 100 \times 0.5 n s)) /0.5 n s = 0.965685$

性能更好了

减小总共的内存访问时间（优势）

会占用内存，不再拥有其他类型功能单元的资源。无法做其他事情（劣势）

5.7.6 [20] <§5.4> In older processors such as the Intel Pentium or Alpha 21264, the second level of cache was external (located on a diff erent chip) from the main processor and the fi rst level cache. While this allowed for large second level caches, the latency to access the cache was much higher, and the bandwidth was typically lower because the second level cache ran at a lower frequency. Assume a 512 KiB off -chip second level cache has a global miss rate of 4%. If each additional 512 KiB of cache lowered global miss rates by 0.7%, and the cache had a total access time of 50 cycles, how big would the cache have to be to match the performance of the second level direct-mapped cache listed above? Of the eight-way set associative cache?

就算L2cache失效率为0。 50ns的访问时间会导致他的AMAT为

0.5

3.5

0.07\times 50\times 0.5ns / 0.5s = 3.5

$0.07 \times 50 \times 0.5 n s /0.5 s = 3.5$

计算的CPI，比上文计算的L2cache的CPI更大，所以不需要改进实现这种cache

原文链接：https://blog.csdn.net/JamSlade/article/details/126539019

5.5